Thành phố định xây cây cầu bắc ngang con sông dài \(500m\), biết rằng người ta định xây cầu có 10 nhịp cầu hình dạng parabol, biết hai bên đầu cầu và giữa mối nhịp nối người ta xây một chân trụ rộng \(5m,\) khoảng cách giữa 2 chân trụ liên tiếp là \(40m\). Bề dày nhịp cầu không đổi là \(20cm\). Biết một nhịp cầu như hình vẽ. Hỏi lượng bê tông để xây các nhịp cầu là bao nhiêu \({{m}^{3}}\)? (kết quả làm tròn đến hàng đơn vị).

Bên trong hình vuông cạnh 4, dựng hình sao bốn cánh đều như hình vẽ bên (các kích thước cần thiết cho như ở trong hình bên). Thể tích \(V\) của khối tròn xoay sinh ra khi quay hình sao đó quanh trục \(Ox\) (làm tròn kết quả đến hàng phần mười) là bao nhiêu?

Gọi D là hình phẳng giới hạn bởi các đường \(y={{x}^{2}}+3\), \(y=0\), \(x=0\), \(x=2\). Thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) bằng:

Cho hai nửa đường tròn như hình vẽ, biết đường kính của đường tròn lớn gấp đôi đường kính của đường tròn nhỏ

Nửa đường tròn đường kính \(AB\) có diện tích là \(32\pi \) và \(\widehat{BAC}={{30}^{0}}\). Ký hiệu \(\left( H \right)\) là hình phẳng được tô màu như trong hình vẽ. Thể tích khối tròn xoay tạo thành khi cho hình \(\left( H \right)\) quay quanh trục \(AB\) bằng bao nhiêu (Làm tròn đến hàng đơn vị)?

Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ a;b \right]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\) được tính theo công thức:

Một bể chứa nhiên liệu hình trụ đặt nằm ngang, có chiều dài 5 m, có bán kính đáy 1 m. Chiều cao của mực nhiên liệu là 1,5 m. Tính thể tích phần nhiên liệu trong bể (theo đơn vị \({{\text{m}}^{3}}\), làm tròn đến chữ số thâph phân hàng phần trục).

Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;b \right]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\) được tính theo công thức:

Một cái trứng khủng long đồ chơi là một khối tròn xoay được tạo thành từ 2 mảnh ghép lại. Biết mảnh trên được tạo thành khi xoay một phần tư đường elip với trục lớn là 8cm và trục nhỏ là 4cm quanh trục \(Ox\) và mảnh dưới được tạo thành khi xoay một phần tư đường tròn bán kính bằng 2cm quanh trục \(Ox\) như hình sau (bỏ qua độ dày của vỏ trứng).

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?

Một bể chứa nhiên liệu hình trụ đặt nằm ngang, có chiều dài 5m, có bán kính đáy 1m. Chiều cao của mực nhiên liệu là 1,5m. Tính thể tích phần nhiên liệu trong bể (theo đơn vị \({{\text{m}}^{3}}\), làm tròn đến chữ số thâph phân hàng phần trục).

Hình vẽ bên mô tả hiệu suất làm việc của hai công nhân trong một nhà máy trong thời gian 6 giờ. Công nhân \(A\) đang sản xuất với hiệu suất \(Q_{1}^{'}\left( t \right)=-2{{t}^{2}}+4t+58\) sản phẩm mỗi giờ, trong khi công nhân \(B\) đang sản xuất với hiệu suất \(Q_{2}^{'}\left( t \right)=53+at\) sản phẩm mỗi giờ \(\left( a\in \mathbb{R} \right)\). Biết rằng hàm \({{Q}_{1}}\left( t \right)\) và \({{Q}_{2}}\left( t \right)\) mô phỏng số lượng sản phẩm mới làm được của công nhân \(A\) và công nhân \(B\) sau \(t\) giờ.

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\), trục \(Ox\) và hai đường thẳng \(x=1\); \(x=4\) khi quay quanh trục hoành được tính bởi công thức nào?

Một vật thể có kích thước và hình dáng như hình vẽ, đáy là hình elip có độ dài trục lớn bằng 6 và độ dài trục bé bằng 4. Khi cắt vật thể bởi mặt phẳng vuông góc với \(Ox\) ta được thiết diện là một tam giác đều. Thể tích của vật thể là \(a\sqrt{b}\), với \(a,b\) là các số nguyên dương. Tính giá trị của biểu thức \(P={{a}^{2}}+{{b}^{2}}\) 

Một đội thi công cầu đường A vừa đấu thầu được dự án xây cầu ở huyện B bắc ngang qua con sông C.

Để hoạch định được số tiền cần chi để đổ bê tông thô đúc cầu, người ta đưa ra bản thiết kế mặt cắt song song của cầu là hình bên dưới (phần tô đậm là phần đổ bê tông, và các đơn vị đều đo bằng mét).

Trong đó phần giới hạn phía dưới là một đồ thị hàm bậc 2 và phần mỏng nhất của cầu là 1 m.

Biết chiều rộng của cầu bằng 9 m. Số tiền (có VAT) ít nhất để đổ bê tông thô đúc cầu là bao nhiêu. Biết mỗi \(1{{m}^{3}}\) bê tông có giá 1.320.000 (Chưa tính VAT 8%). Đơn vị: tỉ đồng, làm tròn đến chữ số thập phân thứ 2).

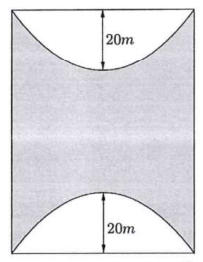
Kiến trúc sư thiết kế một khu sinh hoạt cộng đồng có dạng hình chữ nhật với chiều rộng và chiều dài lần lượt là 60m và 80m. Trong đó, phần được tô màu đậm là sân chơi, phần còn lại để trồng hoa. Mỗi phần trồng hoa có đường biên cong là một phần của parabol với đỉnh thuộc một trục đối xứng của hình chữ nhật và khoảng cách từ đỉnh đó đến trung điểm cạnh tương ứng của hình chữ nhật bằng 20m (xem hình minh họa). Diện tích của phần sân chơi là bao nhiêu mét vuông?

Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = x^3 - 4x\), trục hoành và hai đường thẳng \(x = 0, x = 3\) bằng:

Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hàm số \(y=4-{{x}^{2}}\) và trục hoành.

Thể tích khối tròn xoay được tạo thành khi quay \(\left( H \right)\) xung quanh trục \(Ox\) bằng:

Một người điều khiển ô tô đang ở đường dẫn muốn nhập làn vào đường cao tốc. Khi ô tô cách điểm nhập làn 215 m, tốc độ của ô tô là 54 km/h. 1 giây sau đó, ô tô bắt đầu tăng tốc với tốc độ \(v\left( t \right)=at+b\) (\(a,b\in \mathbb{R},\) \(a>0\)), trong đó \(t\) là thời gian tính bằng giây kể từ khi bắt đầu tăng tốc. Biết rằng ô tô nhập làn cao tốc sau 13 giây và duy trì sự tăng tốc trong 17 giây kể từ khi bắt đầu tăng tốc. Xét tính đúng sai của các phát biểu sau?

Diện tích \(S\) của hình phẳng giới hạn bởi các đường \(y=2{{x}^{2}}\), \(y=-1\), \(x=0\) và \(x=1\) được tính bởi công thức nào sau đây?

Cho khối lăng trụ có diện tích đáy bằng \(5{{\text{a}}^{2}}\) và chiều cao bằng \(6\text{a}\). Thể tích của khối lăng trụ đã cho bằng:

Một tấm kính làm mặt bàn (H1) có hình dáng tam giác đều với 3 đỉnh được làm cong (H2). Biết cạnh tấm kính tam giác ban đầu bằng \(12\left( \text{dm} \right)\). Để cắt góc được đẹp thì người ta dùng đường Parabol \(\left( \text{P} \right):y=-\frac{\sqrt{3}}{4}{{x}^{2}}+5\sqrt{3}\left( \text{H}3 \right)\) có hai nhánh tiếp giáp với hai cạnh của tam giác (H4)

Tính diện tích mặt kính (kết quả được làm tròn đến hàng phần chục).

Ông Duy có một mảnh vườn hình vuông cạnh bằng 8 m. Ông dự định xây một cái bể bơi đặc biệt (phần kẻ sọc trong hình vẽ bên). Biết \(AM=\frac{AB}{4}\), phần đường cong đi qua các điểm \(C,M,N\) là một phần của đường Parabol có trục đối xứng là \(MP\left( MP//AD \right)\) và chi phí để làm bể bơi là 5 triệu đồng \(/{{\text{m}}^{2}}\). Số tiền ông Duy phải trả để xây cái bể bơi đó là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị).