Số phức z = a + bi được biểu diễn trên mặt phẳng phức là tiếp điểm của một tiếp tuyến đi qua gốc tọa độ O(0;0) với đường tròn (C):(x−3)2 + (y−4)2 = 4 trên mặt phẳng phức đó. Khoảng cách từ O đến tiếp điểm bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai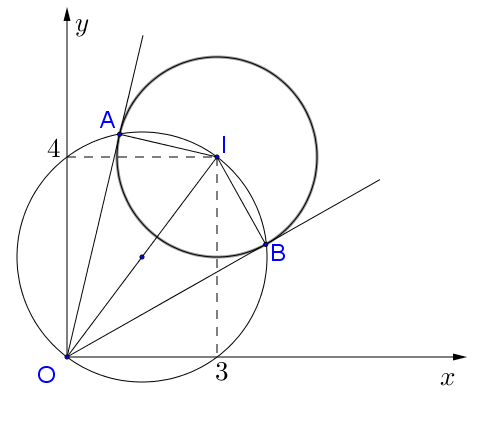
Gọi các tiếp điểm là A và B. Khi đó tọa độ A,B được xác định là giao điểm của đường tròn (C) và đường tròn đường kính OI.
Phương trình đường tròn đường kính OI (tâm I(3;4), bán kính bằng \(\frac{5}{2}):{\left( {x - \frac{3}{2}} \right)^2} + {\left( {y - 2} \right)^2} = \frac{{25}}{4}\)
Do đó tọa độ các tiếp điểm là
\(\begin{array}{l} \left\{ \begin{array}{l} {(x - 3)^2} + {(y - 4)^2} = 4\\ {(x - \frac{3}{2})^2} + {(y - 2)^2} = \frac{{25}}{4} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = \frac{{63 - 8\sqrt {21} }}{{25}};y = \frac{{84 + 6\sqrt {21} }}{{25}}\\ x = \frac{{63 + 8\sqrt {21} }}{{25}};y = \frac{{84 - 6\sqrt {21} }}{{25}} \end{array} \right.\\ \Rightarrow \left| z \right| = \sqrt {21} . \end{array}\)














