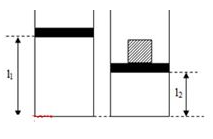
Hai bình có thể tích V1 = 40 lít, V2 = 10 lít thông với nhau bằng một ống có khóa ban đầu đóng. Khóa này chỉ mở nếu p1 ≥ p2 +105 Pa; p1, p2 là áp suất khí trong hai bình. Ban đầu bình 1 chứa khí ở áp suất p0 = 0,9.105 Pa và nhiệt độ T0 = 300K. Trong bình 2 là chân không. Người ta nung nóng đều hai bình từ T0 đến T = 500K. Tới nhiệt độ nào thì khóa mở? Tính áp suất cuối cùng trong bình 2 ?. Chọn đáp án đúng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ Khóa mở: p1 = pm = 105 Pa
+ Đối với bình 1 quá trình diễn ra trước khi K mở là quá trình đẳng tích \( \frac{{{p_0}}}{{{T_0}}} = \frac{{{p_m}}}{{{T_m}}} \to {T_m} = 333K\)
+ Chênh lệch áp suất hai bên sau khi K mở:
\(\Delta p=10^5Pa\)
+ Bình 1 ban đầu: \(p_0V_1=vRT_0\)
+ Sau khi khóa K mở: \((p+\Delta p) V_1=v_1RT\)
+ Ở bình 2 sau khi K mở ta có: \(pV_2=v_2RT\)
+ Mặt khác: \(v=v_1+v_2\)
\(\begin{array}{l} \to \frac{{{p_0}{V_1}}}{{R{T_0}}} = \frac{{(p + \Delta p){V_1}}}{{RT}} + \frac{{p{V_2}}}{{RT}}\\ \Leftrightarrow \frac{{{p_0}{V_1}}}{{{T_0}}} = \frac{{(p + \Delta p){V_1}}}{T} + \frac{{p{V_2}}}{T} = \frac{{({V_1} + {V_2})p + \Delta p{V_1}}}{T}\\ \to p = \frac{{\left( {\frac{{{p_0}T}}{{{T_0}}} - \Delta p} \right){V_1}}}{{{V_1} + {V_2}}} = \frac{{\left( {\frac{{{{0,9.10}^5}.500}}{{300}} - {{10}^5}} \right)40}}{{40 + 10}} = {0,4.10^5}Pa \end{array}\)
Câu hỏi liên quan
-
Có 12g khí chiếm thể tích 4 lít ở 70C. Sau khi nung nóng đẳng áp khối lượng riêng của khí là 1,2g/l. Tìm nhiệt độ khí sau khi nung.
-
Đồ thị như hình vẽ biểu diễn quá trình biến đổi của 3g khí H2. Biết trạng thái đầu khí có nhiệt độ là 170C. Tính nhiệt độ của khí ở trạng thái cuối
-
Khi thể tích bình tăng gấp 10 lần, nhiệt độ giảm đi một nửa thì áp suất của một lượng khí chứa trong bình
-
Một phòng có kích thước 8m x 5m x 4m. Ban đầu không khí trong phòng ở điều kiện tiêu chuẩn, sau đó nhiệt độ của không khí tăng lên tới 100C trong khi áp suất là 78 cmHg. Tính thể tích của lượng khí đã thoát ra khỏi phòng ở điều kiện tiêu chuẩn và khối lượng không khí còn lại ở trong phòng. Khối lượng riêng của không khí ở điều kiện tiêu chuẩn là \({\rho _0} = 1,293\)kg/m3.
-
Một lượng khí Hiđrô đựng trong bình ở áp suất 3atm, nhiệt độ 270C. Đun nóng khí đến 1270C. Do bình hở nên 3/4 lượng khí thoát ra. Áp suất khí trong bình bây giờ là
-
Một xi lanh chứa không khí bị hở vì tiếp xúc với bầu khí quyển.Thể tích khí chiếm chỗ trong xi lanh biến thiên theo nhiệt độ như đồ thị hình vẽ .Kết luận gì về sự biến thiên của khối lượng riêng của khí ?
-
Ở thời kì nén của một động cơ đốt trong 4 kì, nhiệt độ của hỗn hợp khí tăng từ 470C đến 3670C, còn thể tích của khí giảm từ 1,8 lít đến 0,3 lít. Áp suất của khí lúc bắt đầu nén là 100kPa. Coi hỗn hợp khí như chất khí thuần nhất, áp suất cuối thời kì nén là
-
Hai bình cùng dung tích chứa cùng một loại khí với khối lượng m1 và m2 có đồ thị biến đổi áp suất theo nhiệt độ như hình bên. Mối quan hệ giữa m1 và m2 như thế nào ?
.PNG)
-
Trong hệ toạ độ (V-T), đường biểu diễn nào sau đây là đường đẳng áp:
-
Trong xi lanh của một động cơ đốt trong có 2 lít hỗn hợp khí áp dưới áp suất 1,5 atm và nhiệt độ 270C. Pittông nén xuống làm cho thể tích của hỗn hợp khí chỉ còn bằng 0,3 lít và áp suất tăng lên tới 18 atm. Tính nhiệt độ của hỗn hợp khí nén.
-
Quá trình nào dau đây là đẳng quá trình.
-
Phương trình trạng thái của khí lý tưởng đúng cho trường hợp:
-
Quá trình biến đổi trạng thái trong đó áp suất được giữ không đổi gọi là quá trình
-
Trong quá trình đẳng áp thì thể tích của một lượng khí xác định:
-
Một bình thủy tinh có dung tích \(14c{m^3}\) chứa không khí ở nhiệt độ \({77^0}C\)được nối với ống thủy tinh nằm ngang chứa đầy thủy ngân. Đầu kia của ống để hở. Làm lạnh không khí trong bình đến nhiệt độ \({27^0}C\) . Tính khối lượng thủy ngân đã chảy vào bình, dung tích của bình coi như không đổi, khối lượng riêng của thủy ngân là \(13,6\left( {kg/d{m^3}} \right)\)
-
Có một lượng khí lý tưởng đựng trong một xylanh. Áp suất của khí sẽ biến đổi thế nào nếu thể tích của bình tăng gấp 3 lần, còn nhiệt độ tuyệt đối giảm đi một nửa.
-
Một xilanh có pit-tông đóng kín chứa một khối khí ở 30oC, 750 mmHg. Nung nóng khối khí đến 200oC thì thể tích tăng 1,5 lần. Áp suất khí trong xilanh lúc này xấp xỉ bằng
-
Phương trình nào sau đây là phương trình trạng thái của khí lí tưởng ?
-
Một khối khí thay đổi trạng thái như đồ thị biểu diễn. Sự biến đổi khí trên trải qua hai quá trình là nung nóng
-
Một khối khí lý tưởng thực hiện quá trình được biểu diễn như hình vẽ.
.PNG)
Đồ thị nào sau đây cũng biểu diễn quá trình đó?
