Đề thi thử Đánh giá năng lực ĐHQG TP.HCM năm 2025 - Đề 1 - Đề 3
30 câu hỏi 60 phút
Giả sử trong 100 quả táo thì có 15 quả bị sâu và 10 quả có vết bầm tím. Biết rằng chỉ có những quả táo không bị sâu cũng như không bị bầm tím thì mới bán đượHỏi nếu có 5 quả táo vừa bị bầm tím và bị sâu thì trong 100 quả táo đó có thể bán được bao nhiêu quả?
75
70
80
85
Gọi A là tập hợp các quả táo bị sâu và B là tập hợp các quả táo bị bầm tím.
Khi đó số lượng các quả táo không thể bán được là
\(n(A \cup B)=n(A)+n(B)-n(A \cap B)=15+10-5=20\).
Vậy số quả táo có thể bán được là: \(100-20=80\).
Danh sách câu hỏi:
Gọi A là tập hợp các quả táo bị sâu và B là tập hợp các quả táo bị bầm tím.
Khi đó số lượng các quả táo không thể bán được là
\(n(A \cup B)=n(A)+n(B)-n(A \cap B)=15+10-5=20\).
Vậy số quả táo có thể bán được là: \(100-20=80\).
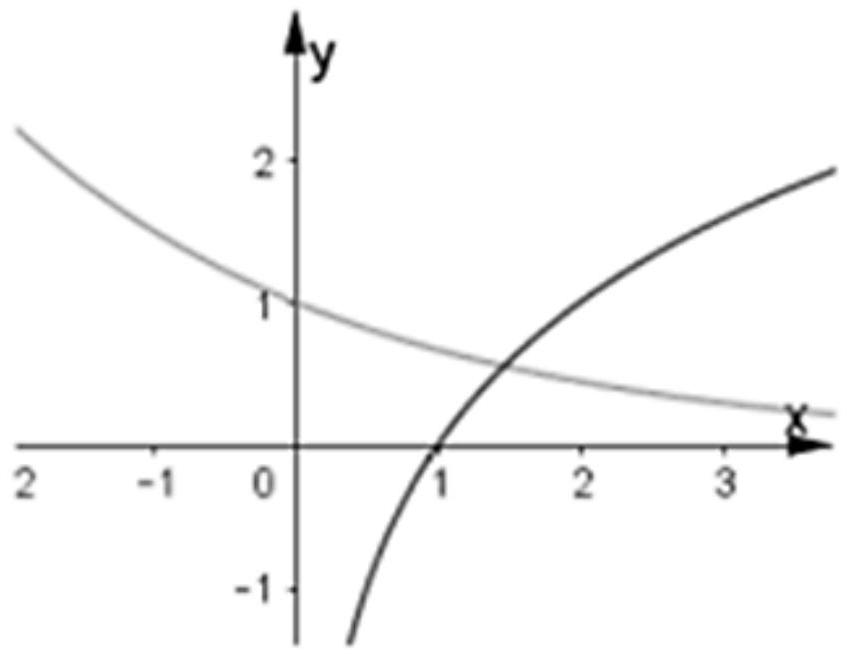
Xét hàm số \(y=a^{x}\) đi qua điểm \((0; 1)\) suy ra đồ thị hàm số là đồ thị của hàm nghịch biến nên \(0<a<1\).
Xét hàm số \(y=\log _{b} x\) đi qua điểm \((1; 0)\) suy ra đồ thị của hàm số là đồ thị của hàm đồng biến nên \(b>1\).
Vậy \(0<a<1<b\).
\(\frac{\sqrt{7}-\sqrt{7-x^{2}}}{\sqrt{x^{2}+16}-4}=\frac{\left(\sqrt{7}-\sqrt{7-x^{2}}\right)\left(\sqrt{x^{2}+16}+4\right)}{x^{2}}\)
\(=\frac{\left(\sqrt{7}-\sqrt{7-x^{2}}\right)\left(\sqrt{x^{2}+16}+4\right)\left(\sqrt{7}+\sqrt{7-x^{2}}\right)}{x^{2}\left(\sqrt{7}+\sqrt{7-x^{2}}\right)}=\frac{x^{2}\left(\sqrt{x^{2}+16}+4\right)}{x^{2}\left(\sqrt{7}+\sqrt{7-x^{2}}\right)}=\frac{\left(\sqrt{x^{2}+16}+4\right)}{\left(\sqrt{7}+\sqrt{7-x^{2}}\right)}\)
Khi đó \(\lim _{x \rightarrow 0} \frac{\sqrt{7}-\sqrt{7-x^{2}}}{\sqrt{x^{2}+16}-4}=\lim _{x \rightarrow 0} \frac{\left(\sqrt{x^{2}+16}+4\right)}{\left(\sqrt{7}+\sqrt{7-x^{2}}\right)}=\frac{4}{\sqrt{7}}\)
Vậy \(T=a+b=4+7=11\).
Áp dụng công thức \((\ln u)^{\prime}=\frac{u^{\prime}}{\ln u}\) và \((\sqrt{u})^{\prime}=\frac{u^{\prime}}{2 \sqrt{u}}\).
Khi đó ta có \(f^{\prime}(x)=\frac{1}{2 x \cdot \ln x \cdot \sqrt{\ln (\ln x)}}\).
Ta có bảng tần số ghép nhóm chứa giá trị đại diện như sau:
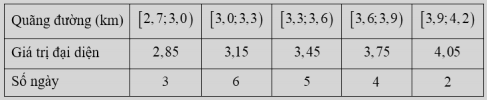
Cỡ mẫu là: \(n=3+6+5+4+2=20\).
Số trung bình của mẫu số liệu là:
\(\bar{x}=\frac{2,85.3+3,15.6+3,45.5+3,75.4+4,05.2}{20}=3,39\).