Đề thi thử Đánh giá năng lực ĐHQG TP.HCM năm 2025 - Đề 2 - Đề 3
30 câu hỏi 60 phút
Họ nguyên hàm của hàm số \(f(x)=3^{2 x-1}\) là
\(\frac{9^{x}}{3}+C\)
\(\frac{9^{x}}{6}+C\)
\(\frac{9^{x}}{6 \ln 3}+C\)
\(\frac{9^{x}}{3 \ln 3}+C\)
Ta có \(f(x)=3^{2 x-1}=\frac{9^{x}}{3}\)
Khi đó \(\int f(x) \mathrm{d} x=\frac{1}{3} \int 9^{x} \mathrm{~d} x=\frac{1}{3} \cdot \frac{9^{x}}{\ln 9}+C=\frac{9^{x}}{6 \ln 3}+C\).
Danh sách câu hỏi:
Ta có \(f(x)=3^{2 x-1}=\frac{9^{x}}{3}\)
Khi đó \(\int f(x) \mathrm{d} x=\frac{1}{3} \int 9^{x} \mathrm{~d} x=\frac{1}{3} \cdot \frac{9^{x}}{\ln 9}+C=\frac{9^{x}}{6 \ln 3}+C\).
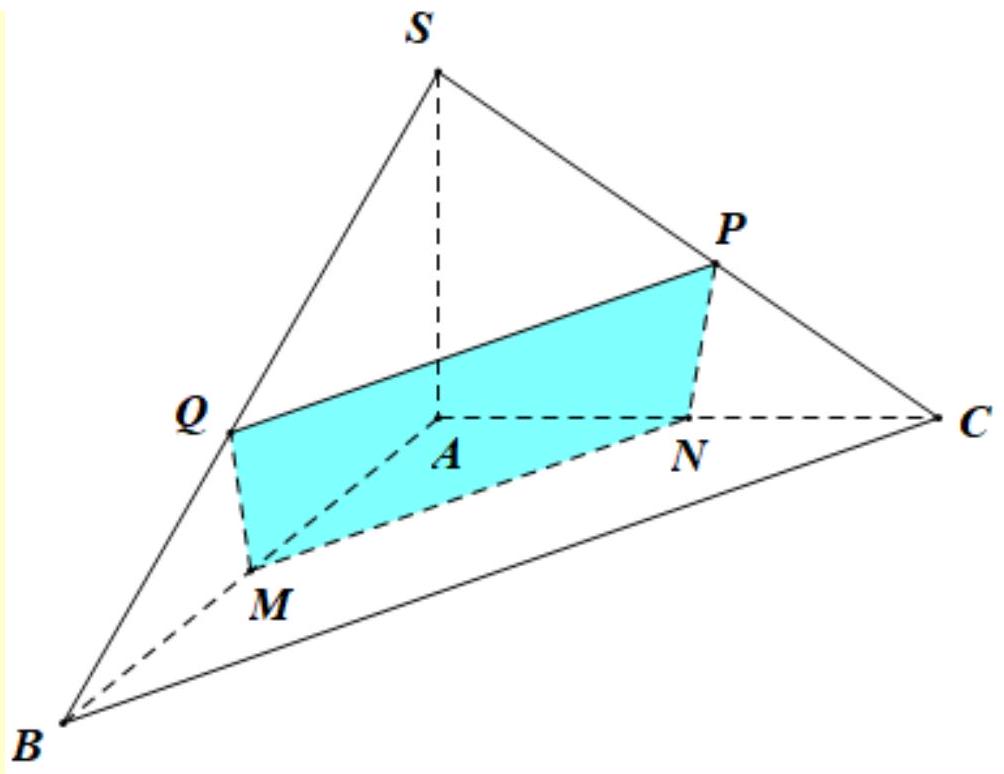
Ta có: \(\left\{\begin{array}{l}A B \perp B C \\ S A \perp B C\end{array} \Rightarrow B C \perp S B\right.\)
Vậy \(\left\{\begin{array}{l}B C \perp S B \\ (P) \perp S B\end{array} \Rightarrow(P) / / B C\right.\)
Mà \((P) \cap(A B C)=M N\)
Từ (1) và (2) \(\Rightarrow M N / / B C\)
Tương tự ta chứng minh được \(P Q / / B C\)
Ta có: \(B C \perp(S A B) \Rightarrow M Q \perp B C\)
Mà \(M Q \perp S B \Rightarrow M Q \perp(S B C) \Rightarrow M Q \perp Q P\)
Vậy thiết diện là hình thang \(M N P Q\) vuông tại \(M, Q\).
Xác suất để trả lời đúng 1 câu là \(\frac{1}{4}\), xác suất để trả lời sai 1 câu là \(\frac{3}{4}\).
Gọi số câu trả lời đúng là \(x(0 \leq x \leq 10, x \in \mathbb{N})\) thì số câu trả lời sai là \(10-x\).
Số điểm học sinh đó đạt được là \(5 x-2(10-x)=7 x-20\).
Theo giả thiết \(\Rightarrow 7 x-20<1 \Leftrightarrow 7 x<21 \Leftrightarrow x<3 \Rightarrow x \in\{0 ; 1 ; 2\}\)
TH1: Đúng 0 câu, sai 10 câu \(P_{1}=\left(\frac{3}{4}\right)^{10}\)
TH2: Đúng 1 câu, sai 9 câu \(P_{2}=C_{10}^{1} \cdot \frac{1}{4} \cdot\left(\frac{3}{4}\right)^{9}\)
TH3: Đúng 2 câu, sai 8 câu \(P_{3}=C_{10}^{2} \cdot\left(\frac{1}{4}\right)^{2} \cdot\left(\frac{3}{4}\right)^{8}\)
Vậy xác suất để học sinh đó nhận điểm dưới 1 là: \(\left(\frac{3}{4}\right)^{10}+C_{10}^{1} \cdot \frac{1}{4} \cdot\left(\frac{3}{4}\right)^{9}+C_{10}^{2} \cdot\left(\frac{1}{4}\right)^{2} \cdot\left(\frac{3}{4}\right)^{8} \approx 0,53\).
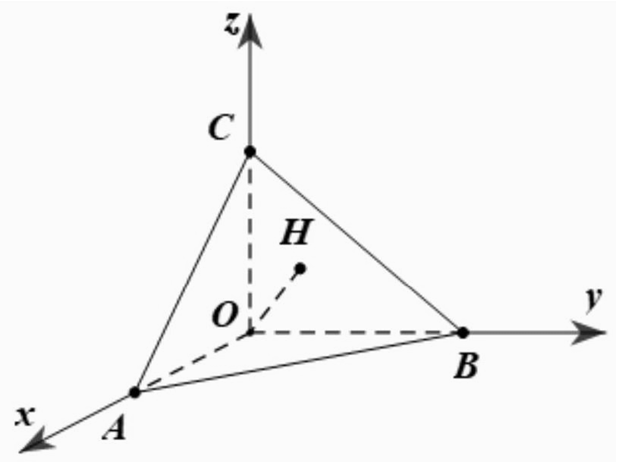
Do \(H\) là trực tâm \(\triangle A B C \Rightarrow A H \perp B C\).
Mặt khác: \(O A \perp(O B C)\) ( do \(O x \perp(O y z)) \Rightarrow O A \perp B C \Rightarrow B C \perp(O A H) \Rightarrow B C \perp O H\).
Chứng minh tương tự ta có: \(A B \perp O H\).
\(\Rightarrow O H \perp(A B C) \Rightarrow \overrightarrow{O H}=(1 ; 3 ; 5)\) là vectơ pháp tuyến của mặt phẳng \((A B C)\) đi qua \(H\).
\(\Rightarrow(A B C): 1(x-1)+3(y-3)+5(z-5)=0 \Leftrightarrow x+3 y+5 z-35=0\).
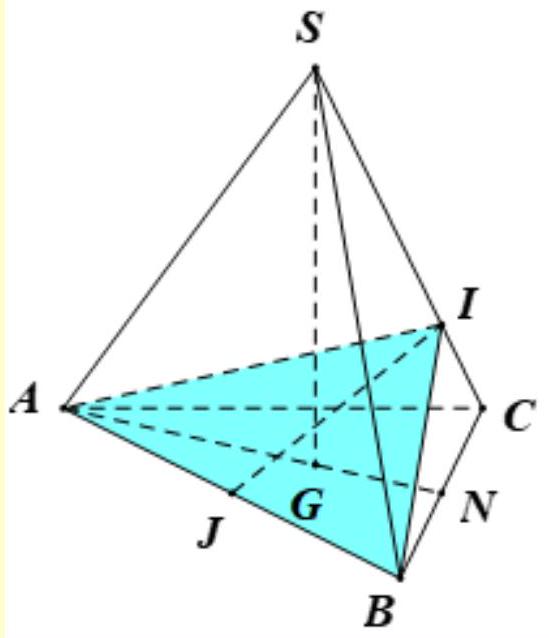
Kẻ \(A I \perp S C \Rightarrow(A I B) \perp S C\). Thiết diện là tam giác \(A I B\)
Ta có \(A I=A C \sin A C S=a \sqrt{1-\cos ^{2} A C S}=a \sqrt{1-\left(\frac{a^{2}+b^{2}-b^{2}}{2 a b}\right)}=\frac{a}{2 b} \sqrt{4 b^{2}-2 a b}\)
Gọi \(J\) là trung điểm của \(A B\). \(\triangle A I B\) cân tại \(I\) suy ra \(I J \perp A B\)
\(I J=\sqrt{A I^{2}-A J^{2}}=\frac{a}{2 b} \sqrt{3 b^{2}-2 a b} \Rightarrow S=\frac{1}{2} A B. I J=\frac{a^{2} \sqrt{3 b^{2}-2 a b}}{4 b}\).