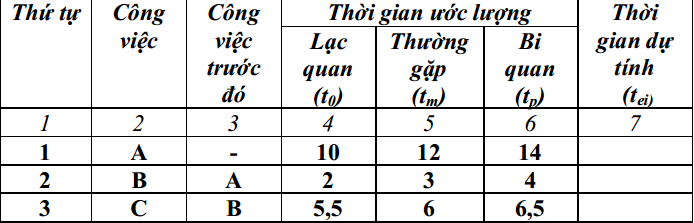
Có bảng tính toán các đại lượng của phương trình đường thẳng dùng dự báo như sau:
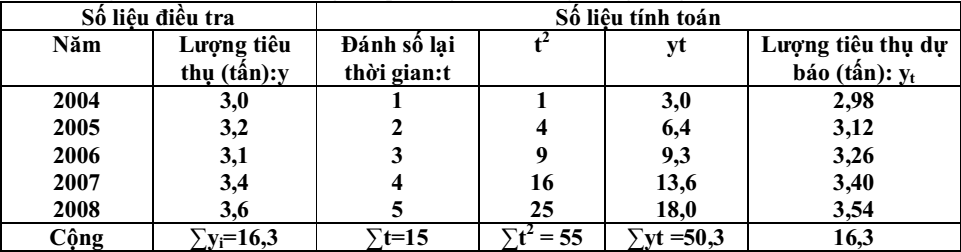
Phương trình đường thẳng dùng dự báo dạng tổng quát là: yt = a0 + a1t và hệ phương trình chuẩn tắc là:
\(\left\{ \begin{array}{l} \sum y = n{a_0} + {a_1}\sum t \\ \sum {yt} = {a_0}\sum t + {a_1}\sum {{t^2}} \end{array} \right.\)
Vậy hệ số a0 bằng:
Trả lời:
Đáp án đúng: B
Từ bảng số liệu, ta có:
\(\sum y = 21.4\)
\(\sum t = 15\)
\(\sum yt = 77.1\)
\(\sum t^2 = 55\)
n = 7
Thay vào hệ phương trình chuẩn tắc:
\(\left\{ \begin{array}{l} 21.4 = 7{a_0} + 15{a_1} \\ 77.1 = 15{a_0} + 55{a_1} \end{array} \right.\)
Giải hệ phương trình, ta được:
a0 = 1.48
a1 = 0.8
Vậy hệ số a0 = 1.48
Tổng hợp 900 câu trắc nghiệm Quản trị dự án có đáp án hay nhất dành cho các bạn sinh viên ôn thi đạt kết quả cao nhất. Mời các các bạn tham khảo!
50 câu hỏi 60 phút