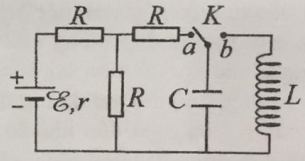
Dùng mạch điện như hình bên để tạo ra dao động điện từ. Ban đầu khóa K vào chốt a, khi dòng điện qua nguồn điện ổn định thì chuyển khóa K đóng sang chốt b. Biết x = 5 V; r = 1 W; R = 2 W; \(L=\frac{1}{\pi }\,mH\) và \(C=\frac{9}{10\pi }\,\mu F\). Lấy 1 e = 1,6.10-19 C. Trong khoảng thời gian 10 ms kể từ thời điểm đóng K vào chốt b, có bao nhiêu electron đã chuyển đến bản tụ điện nối với khóa K?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai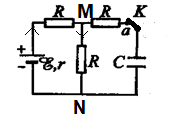
Khi khóa K ở chốt a, ta có hiệu điện thế ở hai đầu tụ điện là :
U0 = UMN = I.R
\(I=\frac{\xi }{2R+r}\to {{U}_{0}}=\frac{\xi }{2R+r}.R=\frac{5}{2.2+1}.2=2\,V\)
Khi khóa K ở chốt b, ta có mạch dao động LC với chu kì:
\(T=2\pi \sqrt{LC}=2\pi \sqrt{\frac{{{10}^{-3}}}{\pi }.\frac{{{9.10}^{-6}}}{10\pi }}={{6.10}^{-5}}s=60\,\mu s\)
Phương trình điện tích khi đóng K vào chốt b là:
q = q0.coswt (C) (j = 0 do ban đầu điện tích cực đại)
Sau thời gian 10 ms :
\(t=10\,\mu s=\frac{T}{6}\) thì \(q=\frac{{{q}_{0}}}{2}\)
Lượng điện tích chuyển đến tụ là: \(\Delta q={{q}_{0}}-\frac{{{q}_{0}}}{2}=\frac{{{q}_{0}}}{2}=\frac{C{{U}_{0}}}{2}\)
Số electron chuyển đến bản tụ là: \(\Delta n=\frac{\Delta q}{e}=\frac{C{{U}_{0}}}{2e}=\frac{\frac{{{9.10}^{-6}}}{10\pi }.2}{2.1,{{6.10}^{-19}}}\approx 1,{{79.10}^{12}}\)