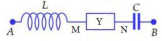
Cho đoạn mạch AB như hình vẽ, cuộn cảm thuần có độ tự cảm L, tụ điện có điện dung C. Đặt vào A, B điện áp xoay chiều \(u={{U}_{0}}\cos \omega t\) thì giá trị điện áp cực đại hai đầu đoạn mạch Y cũng là U0 và các điện áp tức thời uAN lệch pha \(\frac{\pi }{2}\) so với uMB. Biết 4LCω2 = 3. Hệ số công suất của đoạn mạch Y lúc đó là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
\(4LC{{\omega }^{2}}=3\Rightarrow 4\omega L.\omega C=3\Rightarrow \frac{4{{Z}_{L}}}{{{Z}_{C}}}=3\Rightarrow {{Z}_{L}}=\frac{3}{4}{{Z}_{C}}\)
Chuẩn hóa \({{Z}_{C}}=1\Rightarrow {{Z}_{L}}=\frac{3}{4}\)
Giả sử đoạn mạch Y có R, ZL0, ZC0
Điện áp cực đại giữa hai đầu đoạn mạch Y là:
\({{U}_{0Y}}={{U}_{0}}\Rightarrow {{Z}_{Y}}=Z\Rightarrow {{R}^{2}}+{{\left( {{Z}_{L0}}-{{Z}_{C0}} \right)}^{2}}={{R}^{2}}+{{\left( {{Z}_{L}}+{{Z}_{L0}}-{{Z}_{C}}-{{Z}_{C0}} \right)}^{2}}\)
\(\Rightarrow {{Z}_{L0}}-{{Z}_{C0}}=-\left( {{Z}_{L}}+{{Z}_{L0}}-{{Z}_{C}}-{{Z}_{C0}} \right)\Rightarrow {{Z}_{L0}}-{{Z}_{C0}}=\frac{{{Z}_{C}}-{{Z}_{L}}}{2}=\frac{1}{8}\)
Điện áp giữa hai đầu đoạn mạch AN và MB vuông pha, ta có:
\(\tan {{\varphi }_{AN}}.\tan {{\varphi }_{MB}}=-1\Rightarrow \frac{{{Z}_{L}}+{{Z}_{L0}}-{{Z}_{C0}}}{R}\cdot \frac{{{Z}_{L0}}-{{Z}_{C0}}-{{Z}_{C}}}{R}=-1\)
\(\Rightarrow \frac{\frac{3}{4}-\frac{1}{8}}{R}\cdot \frac{\frac{1}{8}-1}{R}=-1\Rightarrow R=\frac{8}{7}\)
Hệ số công suất của đoạn mạch Y là:
\(\cos {{\varphi }_{Y}}=\frac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L0}}-{{Z}_{C0}} \right)}^{2}}}}=\frac{\frac{8}{7}}{\sqrt{{{\left( \frac{8}{7} \right)}^{2}}+{{\left( \frac{1}{8} \right)}^{2}}}}\approx 0,994\)
Đề thi thử THPT QG năm 2021 môn Vật Lý
Trường THPT Lục Nguyên
Câu hỏi liên quan
-
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa 2 khe F1 và F2 là 1 mm, khoảng cách từ màn chứa hai khe đến màn quan sát giao thoa là 2 m. Chiếu ánh sáng gồm 2 bức xạ đơn sắc màu vàng và màu lục có bước sóng lần lượt là 0,6 µm và 0,5 µm vào hai khe thì thấy trên màn quan sát có những vân sáng đơn sắc và các vân sáng cùng màu vân trung tâm. Có bao nhiêu vân màu lục giữa hai vân sáng cùng màu vân trung tâm?
-
Tần số dao động của một con lắc đơn được tính bằng công thức nào sau đây?
-
Trong đoạn mạch xoay chiều, chỉ số của Ampe kế cho biết giá trị nào của dòng điện?
-
Đặt điện áp \(u={{U}_{0}}\cos \left( \omega t+\frac{\pi }{4} \right)\) (U0 không đổi, ω thay đổi được) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Hình bên là đồ thị sự phụ thuộc của giá trị hiệu dụng I của cường độ dòng điện trong mạch theo tần số góc ω, Gọi i1, i2, i3 và i4 là cường độ dòng điện tức thời tương ứng khi ω có giá trị lần lượt là ω1, ω2, ω3 và ω4. Hệ thức nào sau đây đúng?
.png)
-
Một chất điểm dao động điều hòa trên trục Ox có vận tốc bằng 0 tại hai thời điểm liên tiếp t1 = 1,75s và t2 = 2,5s; tốc độ trung bình trong khoảng thời gian đó là 16 cm/s. Ở thời điểm t = 0, chất điểm đang chuyển động ngược chiều dương trục tọa độ ở vị trí có li độ bằng bao nhiêu?
-
Trong thiết bị kiểm tra hành lí ở các sân bay có ứng dụng tia nào sau đây?
-
Một máy phát điện xoay chiều một pha với phần cảm là rôto có p cặp cực. Khi rôto quay đều với tốc độ n (vòng/phút) thì tần số của suất điện động (tính theo đơn vị Hz) do máy phát ra là
-
Tần số dao động riêng của con lắc lò xo gồm lò xo có độ cứng k và vật nặng khối lượng m là
-
Hạt tải điện trong kim loại là
-
Đặt điện áp xoay chiều có tần số f vào hai đầu của một cuộn cảm thuần có độ tự cảm L thì cảm kháng của cuộn cảm là
-
Dao động của một chất điểm là tổng hợp của hai dao động cùng phương cùng tần số có biên độ lần lượt là 5 cm và 8 cm. Biên độ dao động tổng hợp của chất điểm không thể là
-
Trong cấu tạo của máy biến áp, máy tăng áp có tỉ số giữa số vòng dây cuộn thứ cấp và sơ cấp
-
Thiết bị nào sau đây là ứng dụng của hiện tượng cộng hưởng?
-
Trong hiện tượng giao thoa ánh sáng đơn sắc tại vị trí có vân tối trên màn thì hai sóng ánh sáng truyền đến phải
-
Đặt điện áp xoay chiều có giá trị hiệu dụng 100 V vào đoạn mạch R, L, C mắc nối tiếp thì điện áp hiệu dụng ở hai cực tụ điện và ở hai đầu cuộn cảm thuần lần lượt là 130 V và 50 V. Điện áp hiệu dụng giữa hai đầu điện trở là
-
Trên một sợi dây rất dài có hai điểm M và N cách nhau 12 cm. Tại điểm O trên đoạn MN người ta gắn vào dây một cần rung dao động với phương trình \(u=3\sqrt{2}\cos 20\pi t(cm)\)(t tính bằng s), tạo ra sóng truyền trên dây với tốc độ 1,6 m/s. Khoảng cách xa nhất giữa 2 phần tử dây tại M và N khi có sóng truyền qua là
-
Một sóng hình sin có tần số f truyền trong một môi trường với tốc độ v thì có bước sóng là
-
Trong máy quang phổ lăng kính, bộ phận nào gây ra hiện tượng tán sắc ánh sáng?
-
Một vật dao động theo phương trình \(x=4\cos \left( 5\pi t+\frac{\pi }{3} \right)cm.\) Biên độ dao động của vật là
-
Một vật tham gia đồng thời hai dao động điều hoà cùng phương có phương trình lần lượt là \({{x}_{1}}=5\cos \left( 5\pi t+{{\varphi }_{1}} \right)(cm);\text{ }{{x}_{2}}=5\cos \left( 5\pi t+{{\varphi }_{2}} \right)(cm)\)với \(0\le {{\varphi }_{1}}-{{\varphi }_{2}}\le \pi .\) Biết phương trình dao động tổng hợp \(x=5\cos (5\pi t+\pi \text{/6})(cm).\) Giá trị của φ2 là
