ADMICRO
Cho hình chóp S.ABCD có đáy là hình thoi cạnh aa, ∠BAD=600, cạnh bên SA=a và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ B đến mặt phẳng (SCD).
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ADSENSE / 9
Chủ đề: Đề thi Học Kỳ/Giữa Kỳ
Môn: Toán Lớp 12
Lời giải:
Báo sai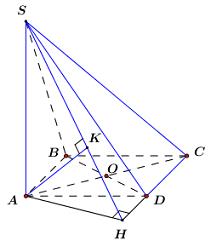
Ta có AB∥CD(gt)⇒AB∥(SCD) ⇒d(B;(SCD))=d(A;(SCD)).
Trong (ABCD) kẻ AH⊥CD.
Vì ∠BAD=600⇒∠ADC=1200 nên điểm H nằm ngoài đoạn thẳng CD.
Trong (SAH) dựng AK⊥SH(H∈SH) ta có:
{CD⊥AHCD⊥SA(SA⊥(ABCD)) ⇒CD⊥(SAH)⇒CD⊥AK.
{AK⊥SHAK⊥CD⇒AK⊥(SCD)⇒d(A;(SCD))=AK.
Xét tam giác vuông AHD có ∠ADH=1800−∠ADC=600, AD=a ⇒AH=AD.sin600=a√32.
Vì SA⊥(ABCD) nên SA⊥AH, suy ra tam giác SAH vuông tại A, áp dụng hệ thức lượng trong tam giác vuông ta có: AK=SA.AH√SA2+AH2 =a.a√32√a2+3a24=a√217.
Vậy d(B;(SCD))=a√217.
Chọn A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề thi giữa HK1 môn Toán 12 năm 2022-2023
Trường THPT Nguyễn Công Trứ
14/06/2025
165 lượt thi
0/40
Bắt đầu thi
ZUNIA12
ZUNIA9
AANETWORK