ADMICRO
Giá trị lớn nhất của hàm số \(y=\frac{1}{\cos x}\) trên khoảng \(\left(\frac{\pi}{2} ; \frac{3 \pi}{2}\right)\) là:
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
ZUNIA12
Lời giải:
Báo sai\(y^{\prime}=\frac{\sin x}{\cos ^{2} x}, y^{\prime}=0 \Leftrightarrow x=\pi\left(x \in\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)\right)\)
Bảng biến thiên
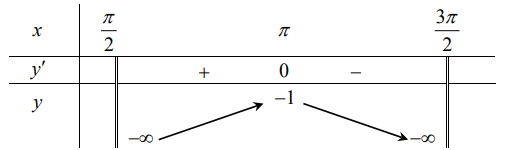
Vậy \(\max\limits _{\left(\frac{\pi}{2} ; \frac{3 \pi}{2}\right)} y=-1 \text { và } \min\limits _{\left(\frac{\pi}{2}, \frac{3 \pi}{2}\right)} y\) không tồn tại.
ZUNIA9
AANETWORK



.jpg.png)
.PNG)
.png)











