ADMICRO
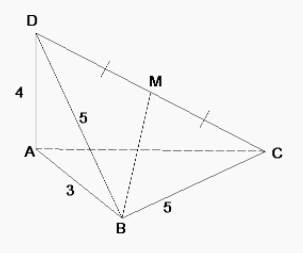
Cho tứ diện ABCD có AD vuông góc mặt phẳng (ABC); AC=AD=4; AB=3; BC=5. Tính khoảng cách từ A đến mặt phẳng (BCD).
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo saiDễ thấy tam giác ABC vuông tại A
Nên:
\(\begin{array}{l} {S_{ABC}} = \frac{1}{2}AB.AC = 6\\ {V_{D.ABC}} = {S_{ABC}}.DA = 8 = {V_{A.BCD}} \end{array}\)
Xét tam giác BCD ta có: \( BC = BD = 5;DC = 4\sqrt 2 \)
Gọi M là trung điểm của DC thì:
\(\begin{array}{l} BM \bot DC \Rightarrow BM = \sqrt {17} \\ \Rightarrow {S_{BCD}} = \frac{1}{2}BM.DC = 2\sqrt {34} \\ \Rightarrow d\left( {A,\left( {DBC} \right)} \right) = \frac{{3.{V_{A.DBC}}}}{{{S_{DBC}}}} = \frac{{12}}{{\sqrt {34} }} \end{array}\)
ZUNIA9
AANETWORK