Cho khối lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác cân với \(A B=A C=a, \widehat{B A C}=120^{\circ}\) Mặt phẳng \(\left(A B^{\prime} C^{\prime}\right)\) tạo với đáy một góc 600 Thể tích của khối lăng trụ đã cho bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai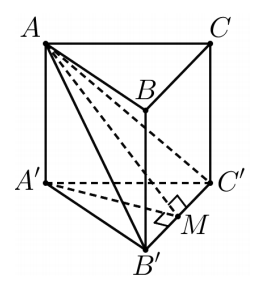
Gọi M là trung điểm của đoạn thẳng B' C' Dễ dàng xác định được
\(60^{\circ}=\left(\widehat{\left(A B^{\prime} C^{\prime}\right),\left(A^{\prime} B^{\prime} C^{\prime}\right)}\right)=\left(\widehat{A M, A^{\prime} M}\right)=\widehat{A M A^{\prime}}\)
Tam giác vuông A' B' M , có
\(A^{\prime} M=A^{\prime} B^{\prime} \cdot \cos \widehat{M A^{\prime} B^{\prime}}=a \cdot \cos 60^{\circ}=\frac{a}{2}\)
Tam giác vuông AA' M , có
\(A A^{\prime}=A^{\prime} M \cdot \tan \widehat{A M A^{\prime}}=\frac{a}{2} \cdot \tan 60^{\circ}=\frac{a \sqrt{3}}{2}\)
Diện tích tam giác: \(S_{\Delta A B C}=\frac{1}{2} A B \cdot A C \cdot \sin \widehat{B A C}=\frac{a^{2} \sqrt{3}}{4}\)
Vậy thể tích khối lăng trụ \(V_{A B C \cdot A^{\prime} B^{\prime} C^{\prime}}=S_{\Delta A B C} \cdot A A^{\prime}=\frac{3 a^{3}}{8}\)
Câu hỏi liên quan
-
Cho hình chóp tứ giác S.ABCD có thể tích bằng V với đáy là hình bình hành. Gọi C’ là trung điểm cạnh SC. Mặt phẳng qua AC’ và song song với BD cắt các cạnh SB,SD lần lượt tại B’; D’. Khi đó thể tích của khối chóp S.A’B’C’D’ bằng
-
Thể tích khối chóp có độ dài đường cao bằng 6, diện tích đáy bằng 8 là
-
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh 2a và A’B = 3a. Tính thể tích khối hộp chữ nhật ABCD.A’B’C’D’ theo a.
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên (SAD) là tam giác cân tại đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa cạnh bên SB và mặt đáy là 60o. Tính thể tích khối chóp S.ABCD
-
Cho lăng trụ tam giác đều \(ABCD.A'B'C'\) có tất cả các cạnh bằng a. M là trung điểm cạnh \(AB.\) Mặt phẳng (P) đi qua M và vuông góc với CB’, cắt các cạnh BC, CC’, AA’ lần lượt tại N, E, F. Xác định N, E, F và tính thể tích khối chóp \(C.MNEF.\)
-
Cho hình lập phương ABCD.A’B’C’D’. Tính thể tích V của hình lập phương biết rằng khoảng cách từ trung điểm I của AB đến mặt phẳng \(\left( {A’B’CD} \right)\) bằng \(\frac{a}{{\sqrt 2 }}\)
-
Cho hình lập phương có cạnh bằng 1. Diện tích của mặt cầu ngoại tiếp hình lập phương đó bằng
-
Cho hình chóp S.ABC có \( SA = SB = SC = a\sqrt 3 ;AB = AC = a;BC = 3a\). Thể tích khối chóp S.ABC bằng:
-
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy \(\left( {ABC} \right)\). Biết SA = a, tam giác ABC là tam giác vuông cân tại A, AB = 2a. Tính theo a thể tích V của khối chóp S.ABC.
-
Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Tính thể tích của (H).
-
Cho hình chóp O.ABC có OA, OB, OC đôi một vuông góc tại O và OA = 2, OB = 3, OC = 6. Thể tích của khối chóp bằng:
-
Cho lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a. Gọi N, I lần lượt là trung điểm của AB, BC; góc giữa hai mặt phẳng (C’AI) và (ABC) bằng \({{60}^{o}}\). Tính theo a thể tích khối chóp NAC’I?
-
Cho khối tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = AC = 2a, AD = 3a. Thể tích V của khối tứ diện đó là:
-
Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác đều cạnh bằng \(a\) và \(\left( {A}'BC \right)\) hợp với mặt đáy \(ABC\) một góc \({{30}^{0}}\). Tính thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\) là
-
Một khối lập phương có độ dài đường chéo bằng a√6a6. Tính thể tích khối lập phương đó.
-
Cho hình lập phương ABCD.A’B’C’D’ có diện tích mặt chéo ACC’A’ bằng \(2\sqrt{2}{{a}^{2}}\). Thể tích của khối lập phương ABCD.A'B'C'D' là:
-
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, \(AB = a\sqrt 5 \), AC = a. Cạnh bên SA = 3a và vuông góc với mặt phẳng \(\left( {ABC} \right)\). Tính thể tích khối chóp S.ABC.
-
Trong các mệnh đề sau, mệnh đề nào sai?
-
Cho khối hộp chữ nhật ABCD.A'B'C'D' có thể tích bằng 2110. Biết A'M = MA; DN = 3ND'D; CP = 2PC'. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằn
-
Cho hình hộp \(ABCD.A'B'C'D'\) có thể tích là \(V.\) Gọi \(M,N,Q\) lần lượt là trung điểm của AD, DC và B’C’. Thể tích của khối tứ diện QBMN bằng:
