Tuyển Tập Đề Thi Tham Khảo Tốt Nghiệp THPT Quốc Gia Năm 2025 - Toán - Bộ Đề 05 - Đề Số 03
Câu 1
Nguyên hàm của hàm số \(y={{2}^{x}}\) là:
A.\(\int{{{2}^{x}}\text{d}x=\ln {{2.2}^{x}}+C}\).
B.\(\int{{{2}^{x}}\text{d}x={{2}^{x}}+C}\).
C.\(\int{{{2}^{x}}\text{d}x=\frac{{{2}^{x}}}{\ln 2}+C}\).
D.\(\int{{{2}^{x}}\text{d}x=\frac{{{2}^{x}}}{x+1}+C}\).
Câu 2
Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;b \right]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,\,\,x=b\) được tính theo công thức:
A.\(S=\int\limits_{a}^{b}{\left| f\left( x \right) \right|}\,\text{d}x\).
B.\(S=\int\limits_{a}^{b}{f\left( x \right)}\,\text{d}x\).
C.\(S=-\int\limits_{a}^{b}{f\left( x \right)}\,\text{d}x\).
D.\(S=\int\limits_{b}^{a}{\left| f\left( x \right) \right|}\,\text{d}x\).
Câu 3
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.\(\left[ 7;\text{ }9 \right)\).
B.\(\left[ 9;\text{ }11 \right)\).
C.\(\left[ 11;\text{ }13 \right)\).
D.\(\left[ 13;\text{ }15 \right)\).
Câu 4
Trong không gian \(Oxyz\), cho hai điểm \(M\left( 1\,;\,2;1 \right)\) và \(N\left( 3;1;-2 \right)\). Đường thẳng \(MN\) có phương trình là:
A.\(\frac{x+1}{4}=\frac{y+2}{3}=\frac{z+1}{-1}\).
B.\(\frac{x-1}{2}=\frac{y-2}{-1}=\frac{z-1}{-3}\).
C.\(\frac{x-1}{4}=\frac{y-2}{3}=\frac{z-1}{-1}\).
D.\(\frac{x+1}{2}=\frac{y+2}{-1}=\frac{z+1}{-3}\).
Câu 5
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
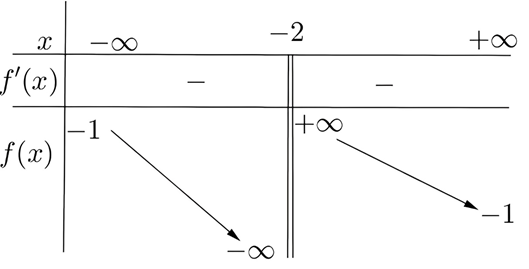
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:
A.\(x=-1\).
B.\(y=-1\).
C.\(y=-2\).
D.\(x=-2\).
Câu 6
Với \(a\) là số thực dương tùy ý, \({{\log }_{4}}\left( 4a \right)\) bằng:
A.\(1-{{\log }_{4}}a\).
B.\(1+{{\log }_{4}}a\).
C.\(4-{{\log }_{4}}a\).
D.\(4+{{\log }_{4}}a\).
Câu 7
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):\,{{\left( x-2 \right)}^{2}}+{{\left( y+1 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=4\).
Tâm của \(\left( S \right)\) có tọa độ là:
A.\(\left( -2;1;-3 \right)\).
B.\(\left( -4;2;-6 \right)\).
C.\(\left( 4;-2;6 \right)\).
D.\(\left( 2;-1;3 \right)\).
Câu 8
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), cạnh bên \(SA\) vuông góc với đáy. Khẳng định nào sau đây đúng?
A.\(AC\bot \left( SBC \right)\).
B.\(BC\bot \left( SAC \right)\).
C.\(BC\bot \left( SAB \right)\).
D.\(AB\bot \left( SBC \right)\).
Câu 9
Tập nghiệm của bất phương trình \({{2}^{x}}\le 4\) là:
A.\(\left( -\infty ;\,2 \right]\).
B.\(\left[ 0;\,2 \right]\).
C.\(\left( -\infty ;\,2 \right)\).
D.\(\left( 0;\,2 \right)\).
Câu 10
Cho cấp số nhân \(\left( {{u}_{n}} \right)\) với \({{u}_{1}}=2\) và công bội \(q=3\). Tìm số hạng thứ \(4\) của cấp số nhân?
A.\(24\).
B.\(54\).
C.\(162\).
D.\(48\).
Câu 11
Cho hình lập phương \(ABCD.A'B'C'D'\) (minh họa như hình bên). Mệnh đề nào sau đây sai?
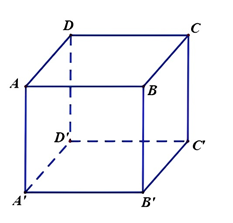 A.
A.\(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}\).
B.\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\).
C.\(\left| \overrightarrow{AB} \right|=\left| \overrightarrow{CD} \right|\).
D.\(\overrightarrow{AB}=\overrightarrow{CD}\).
Câu 12
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm như sau

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.\(\left( -3;0 \right)\).
B.\(\left( 0;+\infty \right)\).
C.\(\left( 0;2 \right)\).
D.\(\left( -\infty ;-3 \right)\).
Câu 13
Cho hàm số \(f\left( x \right)=\sin 2x-x\).
a) \(f\left( -\frac{\pi }{2} \right)=\frac{\pi }{2};f\left( \frac{\pi }{2} \right)=-\frac{\pi }{2}\).
b) Đạo hàm của hàm số đã cho là \({f}'\left( x \right)=\cos 2x-1\).
c) Nghiệm của phương trình \({f}'\left( x \right)=0\) trên đoạn \(\left[ -\frac{\pi }{2};\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right]\) là \(-\frac{\pi }{6}\) hoặc \(\frac{\pi }{6}\).
d) Giá trị nhỏ nhất của \(f\left( x \right)\) trên đoạn \(\left[ -\frac{\pi }{2};\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right]\) là \(-\frac{\pi }{2}\).
Câu 14
Một ô tô bắt đầu chuyển động thẳng nhanh dần đều với tốc độ \(v\left( t \right)=5t\ \ (\text{m/s});\)trong đó \(t\) là thời gian tính bằng giây kể từ khi ô tô bắt đầu chuyển động. Đi được 6 (s) người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a=-\,5\ (\text{m/}{{\text{s}}^{2}})\).
a) Tốc độ của ô tô tại thời điểm 10 (s) tính từ lúc xuất phát là 10\((\text{m/s})\).
b) Quãng đường ô tô chuyển động được trong 6 giây đầu tiên là \(80\ \text{m}\).
c) Quãng đường \(S\) (đơn vị: mét) mà ô tô chuyển động được kể từ lúc bắt đầu đạp phanh đến khi dừng lại được tính theo công thức \(S=\int_{0}^{6}{(30-5t)}dt\).
d) Quãng đường ô tô chuyển động được kể từ lúc bắt đầu chuyển động cho đến khi dừng lại là \(170\,\text{m}\text{.}\)
Câu 15
Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là \(0,4\) và khả năng thắng thầu của dự án 2 là \(0,5\). Khả năng thắng thầu cả 2 dự án là \(0,3\).
Gọi \(A\) là biến cố: “Thắng thầu dự án 1”
Gọi \(B\) là biến cố: “Thắng thầu dự án 2”.
Khi đó:
a) \(A\) và \(B\) là hai biến cố độc lập.
b) Xác suất để công ty thắng thầu đúng 1 dự án bằng \(0,7\).
c) Xác suất để công ty thắng thầu dự án 2 biết công ty thắng thầu dự án 1 là \(0,75\).
d) Xác suất để công ty thắng thầu dự án 2 biết công ty không thắng thầu dự án 1 là \(0,25.\)
Câu 16
Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm \(A\left( 10;~3;0 \right)\) và chuyển động đều theo đường cáp có véc tơ chỉ phương \(\vec{u}=\left( 2;-2;1 \right)\) (hướng chuyển động cùng chiều với hướng véc tơ \(\vec{u}\) với tốc độ là \(4,5\ (\text{m/s});\) (đơn vị trên mỗi trục là mét).
a) Phương trình tham số của đường cáp là: \(\left\{ \begin{align} & x=10+2t \\ & y=3-2t \\ & z=t \\ \end{align} \right.\text{, }\left( t\in \mathbb{R} \right)\).
b) Giả sử sau thời gian t (s) kể từ khi xuất phát (\(t\ge 0\)), cabin đến điểm M. Khi đó tọa độ điểm M là \(M(3t+10;~-3t+3;~\frac{3t}{2}\) ).
c) Cabin dừng ở điểm B có hoành độ \({{x}_{B}}=550\), khi đó quãng đường AB dài 800m.
d) Đường cáp AB tạo với mặt phẳng (Oxyz) một góc \({{30}^{o}}\).
Top 10/15 lượt thi
| Tên | Điểm | Thời gian |
|---|---|---|
| 3.95đ | 18:06 | |
| 3.95đ | 29:16 | |
| 3.85đ | 10:30 | |
| 2.5đ | 07:04 | |
| 2.5đ | 23:08 | |
| 2.2đ | 17:20 | |
| 1.85đ | 01:24 | |
| 1.7đ | 39:12 | |
| 1.3đ | 08:30 | |
| 1.2đ | 01:43 |