Tuyển Tập Đề Thi Tham Khảo Tốt Nghiệp THPT Quốc Gia Năm 2025 - Toán - Bộ Đề 04 - Đề Số 05
Câu 1
Nguyên hàm của hàm số \(f\left( x \right)={{x}^{3}}\) là:
A.\(4{{x}^{4}}+C\).
B.\(3{{x}^{2}}+C\).
C.\({{x}^{4}}+C\).
D.\(\frac{1}{4}{{x}^{4}}+C\).
Câu 2
Gọi \(D\) là hình phẳng giới hạn bởi các đường \(y={{e}^{x}},y=0,x=0\) và \(x=1\). Thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) bằng
A.\(\pi \int\limits_{0}^{1}{{{\text{e}}^{2x}}\text{d}x}\).
B.\(\pi \int\limits_{0}^{1}{{{\text{e}}^{x}}\text{d}x}\).
C.\(\int\limits_{0}^{1}{{{\text{e}}^{x}}\text{d}x}\).
D.\(\int\limits_{0}^{1}{{{\text{e}}^{2x}}\text{d}x}\).
Câu 3
Cho mẫu số liệu ghép nhóm được cho ở bảng sau
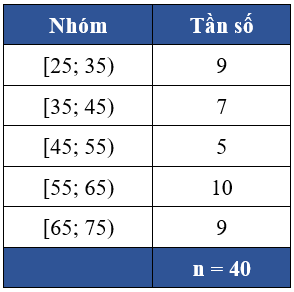
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười) là:
A.\(15,1\).
B.\(15,0\).
C.\(14,8\).
D.\(14,9\).
Câu 4
Trong không gian \(\text{Ox}yz\), phương trình của đường thẳng đi qua \(A\left( -1;-1;1 \right)\) và có một một vectơ chỉ phương \(\vec{u}(1;2;3)\) là:
A.\(\frac{x-1}{1}=\frac{y-1}{2}=\frac{z+1}{3}.\)
B.\(\frac{x+1}{-1}=\frac{y+2}{-1}=\frac{z+3}{1}\).
C.\(\frac{x+1}{1}=\frac{y+1}{2}=\frac{z-1}{3}\).
D.\(\frac{x-1}{-1}=\frac{y-2}{-1}=\frac{z-3}{1}\).
Câu 5
Cho hàm số \(y=\frac{ax+b}{cx+d}(c\ne 0,ad-bc\ne 0)\) có đồ thị như hình vẽ bên. Tiệm cận đứng của đồ thị hàm số là:
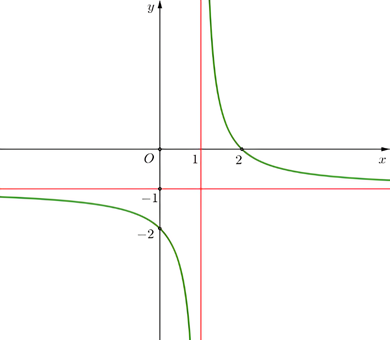 A.
A.\(y=1\).
B.\(x=-1\).
C.\(x=1\).
D.\(y=-1\).
Câu 6
Tập nghiệm của bất phương trình \({{\log }_{5}}\left( 2x-1 \right)<{{\log }_{5}}\left( x+2 \right)\) là:
A.\(S=\left( 3;+\infty \right)\).
B.\(S=\left( -\infty ;3 \right)\).
C.\(S=\left( \frac{1}{2};3 \right)\).
D.\(S=\left( -2;3 \right)\).
Câu 7
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):\,2x-y+z-3=0\). Véctơ nào dưới đây là một véctơ pháp tuyến của mặt phẳng \(\left( P \right)\)?
A.\(\overrightarrow{{{n}_{4}}}=\left( -2;1;1 \right)\).
B.\(\overrightarrow{{{n}_{3}}}=\left( 2;1;1 \right)\).
C.\(\overrightarrow{{{n}_{2}}}=\left( 3;-1;-1 \right)\).
D.\(\overrightarrow{{{n}_{1}}}=\left( -2;1;-1 \right)\).
Câu 8
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông và \(SA\bot \left( ABCD \right)\). Đường thẳng \(BC\) vuông góc với mặt phẳng nào sau đây?
A.\(\left( SAB \right)\).
B.\(\left( SBC \right)\).
C.\(\left( SCD \right)\).
D.\(\left( SBD \right)\).
Câu 11
Cho hình hộp \(ABCD.{A}'{B}'{C}'{D}'\). Khẳng định nào sai trong các khẳng định sau?
 A.
A.\(\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{BD'}\).
B.\(\overrightarrow{A{C}'}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}'}\).
C.\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{C{C}'}=\overrightarrow{AC'}\).
D.\(\overrightarrow{AB}+\overrightarrow{A{A}'}=\overrightarrow{AD}+\overrightarrow{D{D}'}\).
Câu 12
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.\(\left( 0;+\infty \right)\).
B.\(\left( 0;2 \right)\).
C.\(\left( -2;0 \right)\).
D.\(\left( -\infty ;-2 \right)\).
Câu 13
Cho hàm số \(y={{x}^{3}}-3x+1\).
a) Hàm số đồng biến trên \(\left( 1;+\infty \right)\).
b) Hàm số có giá trị cực tiểu bằng 3.
c) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1.
d) Giá trị lớn nhất của hàm số trên \(\left[ -2;1 \right]\) bằng 3.
Câu 14
Một ô tô đang chạy với tốc độ \(108\,km\text{/}h\) thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường. Người lái xe phản ứng một giây sau đó bằng cách đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ \(v\left( t \right)=-10t+30\,\,\left( m\text{/}s \right)\), trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi \(s\left( t \right)\) là quãng đường xe ô tô đi được trong \(t\left( s \right)\) kể từ lúc đạp phanh.
a) Công thức biểu diễn hàm số \(s\left( t \right)=-5{{t}^{2}}+30t\left( m \right)\).
b) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là \(6\) giây.
c) Sau 3 giây kể từ lúc đạp phanh, quãng đường xe ô tô di chuyển được là \(45\left( m \right)\).
d) Quãng đường xe ô tô đã di chuyển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến khi xe ô tô dừng hẳn là \(120\left( m \right)\).
Câu 15
Một công ty truyền thông đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,5 và dự án 2 là 0,6. Khả năng thắng thầu của cả 2 dự án là 0,4. Gọi\(A,\,B\) lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
a) Xác suất \(P(\overline{A})=0,5\) và \(P(\overline{B})=0,4\).
b) Xác suất công ty thắng thầu đúng 1 dự án là \(0,3\).
c) Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là \(0,4\).
d) Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là \(0,8\).
Câu 16
Một máy bay đang di chuyển về phía sân bay. Tại thời điểm hiện tại, vị trí của máy bay là \(B(150;150;5000)\) (trong đó \(5000m\) là độ cao của máy bay so với mặt đất). Máy bay đang di chuyển thẳng tới sân bay với vận tốc \(700\,km/h\). Sân bay có tọa độ\(C(0;0;0)\) và máy bay đang tiến dần đến vị trí hạ cánh tại sân bay.
a) Phương trình tham số của đường thẳng mà máy bay di chuyển theo là \(\left\{ \begin{align} & x=150-150t \\ & y=150-150t \\ & z=5000-5000t \\ \end{align} \right.\)
b) Khoảng cách từ vị trí hiện tại của máy bay \(B(150;150;5000)\) đến sân bay \(C(0;0;0)\) là\(\sqrt{15250000}\approx 3905,6km\).
c) Với vận tốc trung bình của máy bay là \(700\)km/h, thời gian để máy bay hạ cách là khoảng 5,5 giờ.
d) Nếu hệ thống kiểm soát không lưu yêu cầu liên lạc với máy bay khi nó còn cách sân bay 40km thì khi máy bay ở vị trí \(\left( 6;6;200 \right)\) nó còn cách sân bay là \(40\)km.
Top 10/0 lượt thi
| Tên | Điểm | Thời gian |
|---|