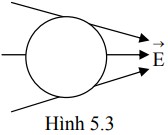
Mặt phẳng tam giác vuông ABC (\(\widehat A\) = 90⁰, BC = 5 cm, AC = 3 cm) song song với đường sức của điện trường đều. Biết E = 5.10³ V/m và các đường sức song song với AB, hướng từ A đến B. Hiệu điện thế:

U_CA = 0

U_AC = +150 V

U_BC = +250 V

U_CB = +250 V.

Trả lời:

Đáp án đúng: A

Tam giác ABC vuông tại A, nên ta có AB = \(\sqrt{BC^2 - AC^2}\) = \(\sqrt{5^2 - 3^2}\) = 4 cm = 0.04 m. Vì các đường sức song song với AB và hướng từ A đến B, nên \(U_{AC}\) = 0 V (do A và C nằm trên cùng một đường đẳng thế). Hiệu điện thế \(U_{BC}\) = \(U_{BA}\) = E.d = 5.10³ * 0.04 = 200 V. Suy ra, \(U_{CB}\) = -\(U_{BC}\) = -200 V. Không có đáp án nào trùng khớp với kết quả tính toán, tuy nhiên, theo cách đặt câu hỏi và các phương án trả lời, có thể đây là một lỗi đánh máy. Trong trường hợp này, nếu đề bài hỏi UBA thì đáp án đúng là: UBA = +200V. Tuy nhiên đề bài lại hỏi UCA, UBC, UAC, UCB nên ta xem xét: UCA = 0 (do C và A nằm trên cùng một đường đẳng thế), UAC = 0 (do A và C nằm trên cùng một đường đẳng thế), UCB = -UBC = -200 V, UBC = -UCB = 200V. Như vậy không có đáp án nào chính xác.

520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Phần 3

500+ câu hỏi ôn tập trắc nghiệm môn Vật lý đại cương sẽ là đề cương ôn thi hữu ích dành cho các bạn sinh viên Đại học - Cao đẳng ôn thi môn đại cương dễ dàng hơn. Mời các bạn cùng tham khảo!

50 câu hỏi 60 phút

Bắt đầu thi

Câu hỏi liên quan

Câu 15:

Ba điện tích điểm +5.10^–9 C, – 6.10^–9 C, +12.10^–9 C đặt tại ba đỉnh tam giác đều cạnh a = 20 cm trong không khí. Chọn gốc điện thế ở vô cùng. Tính công của lực điện trường khi đưa một electron từ rất xa đến trọng tâm tam giác.

Lời giải:

Đáp án đúng: A

Điện thế tại trọng tâm tam giác đều do ba điện tích gây ra là: V = V1 + V2 + V3 = k(q1/r + q2/r + q3/r). Khoảng cách từ mỗi đỉnh đến trọng tâm là r = a/√3.
Vậy V = 9.10^9 * (5.10^-9 - 6.10^-9 + 12.10^-9) / (0.2/√3) = 9.10^9 * 11.10^-9 * √3 / 0.2 = 286.17 V.
Công của lực điện khi di chuyển electron từ vô cực đến trọng tâm là A = qV = -1.602.10^-19 * 286.17 = -4.58 * 10^-17 J.
Chuyển đổi sang eV: A = -4.58 * 10^-17 / (1.602 * 10^-19) = -285.9 eV. Không có đáp án nào khớp, tuy nhiên, có lẽ có sự nhầm lẫn đơn vị trong các đáp án hoặc sai số làm tròn trong quá trình tính toán. Đáp án gần nhất về độ lớn là đáp án C, nhưng dấu lại ngược. Vì vậy, không có đáp án đúng trong các lựa chọn đã cho.

Câu 16:

Mặt phẳng (P) rộng vô hạn, tích điện đều với mật độ σ < 0. Kết luận nào sau đây là SAI?

Lời giải:

Đáp án đúng: A

Mặt phẳng tích điện đều rộng vô hạn tạo ra một điện trường đều, có các đặc điểm sau:

* Cường độ điện trường: Không phụ thuộc vào khoảng cách đến mặt phẳng. Vì vậy, càng gần hay càng xa (P), điện trường vẫn có độ lớn như nhau.
* Hướng của điện trường: Vectơ cường độ điện trường luôn vuông góc với mặt phẳng (P). Vì σ < 0, điện trường hướng vào (P).
* Điện thế: Do điện trường đều, điện thế biến thiên tuyến tính (hàm bậc nhất) với khoảng cách từ mặt phẳng. Vì điện trường hướng vào (P) và σ < 0, nên khi càng xa (P), điện thế càng giảm.

Vậy, phát biểu SAI là: Càng gần (P), điện trường càng mạnh.

Câu 17:

Đặt phân tử có mômen lưỡng cực p_e = 6,24.10^–30 Cm vào điện trường đều E = 3.10⁴ V/m, sao cho \(\overrightarrow {{p_e}}\) hợp với \(\overrightarrow {{E}}\) một góc 30⁰. Tính độ lớn của mômen ngẫu lực tác dụng lên phân tử.

Lời giải:

Đáp án đúng: D

Mômen ngẫu lực tác dụng lên phân tử được tính theo công thức:

M = p_e.E.sin(α)

Trong đó:

- p_e là mômen lưỡng cực của phân tử (6,24.10^–30 Cm)

- E là cường độ điện trường đều (3.10⁴ V/m)

- α là góc giữa vectơ mômen lưỡng cực và vectơ cường độ điện trường (30⁰)

Thay số vào, ta được:

M = 6,24.10^–30 * 3.10⁴ * sin(30⁰) = 6,24.10^–30 * 3.10⁴ * 0,5 = 9,36.10^–26 Nm

Vậy đáp án đúng là 9,36.10^–26 Nm.

Câu 18:

Đĩa tròn phẳng, bán kính a, tích điện đều, mật độ điện mặt σ > 0, trong không khí. Biết \({E_M} = \frac{\sigma }{{2{\varepsilon _0}}}(1 - \frac{h}{{\sqrt {{a^2} + {h^2}} }})\) là trị số cường độ điện trường tại điểm M trên trục của đĩa, cách tâm O một đoạn h. Chọn gốc điện thế ở vô cùng. Biểu thức điện thế tại M là:

Lời giải:

Đáp án đúng: A

Câu 19:

Điện tích phân bố đều trong khối cầu bán kính R, mật độ điện khối ρ. Hằng số điện môi ở trong và ngoài khối cầu đều bằng ε. Xét điểm M cách đều tâm O và mặt cầu. Điểm A nằm trên mặt cầu. Hiệu điện thế U_MA là:

Lời giải:

Đáp án đúng: B

Điểm M cách đều tâm O và mặt cầu, suy ra OM = R/2. Điểm A nằm trên mặt cầu, vậy OA = R.
Điện thế tại điểm M nằm trong khối cầu được tính bằng công thức:
\(V_M = \frac{\rho}{6\varepsilon_0\varepsilon}(3R^2 - r^2) = \frac{\rho}{6\varepsilon_0\varepsilon}(3R^2 - (R/2)^2) = \frac{\rho}{6\varepsilon_0\varepsilon}(3R^2 - R^2/4) = \frac{\rho}{6\varepsilon_0\varepsilon}(\frac{11R^2}{4}) = \frac{11\rho R^2}{24\varepsilon_0\varepsilon}\)
Điện thế tại điểm A nằm trên mặt cầu (r = R) được tính bằng công thức:
\(V_A = \frac{\rho}{6\varepsilon_0\varepsilon}(3R^2 - R^2) = \frac{\rho}{6\varepsilon_0\varepsilon}(2R^2) = \frac{\rho R^2}{3\varepsilon_0\varepsilon}\)
Hiệu điện thế giữa M và A là:
\(U_{MA} = V_M - V_A = \frac{11\rho R^2}{24\varepsilon_0\varepsilon} - \frac{\rho R^2}{3\varepsilon_0\varepsilon} = \frac{11\rho R^2 - 8\rho R^2}{24\varepsilon_0\varepsilon} = \frac{3\rho R^2}{24\varepsilon_0\varepsilon} = \frac{\rho R^2}{8\varepsilon_0\varepsilon}\)
Vậy đáp án đúng là \(\frac{{\rho .{R^2}}}{{8\varepsilon {\varepsilon _0}}}\)\)

Câu 20:

Một quả cầu kim loại có bán kính R = 50 cm, đặt trong chân không, được tích điện Q = 5.10 ^–6C. Tính điện thế tại tâm của quả cầu, chọn gốc điện thế ở vô cùng.

Lời giải: