Khi tính ứng suất tại một điểm bất kỳ trong nền đất chịu tác dụng của tải trọng tập trung đặt trên mặt đất ta dùng công thức nào:

Bài toán không gian trong xác định ứng suất nền đất xét đến sự phân bố ứng suất theo cả ba chiều. Tải trọng dưới đáy móng đơn là một ví dụ điển hình, vì tải trọng tập trung và lan truyền theo mọi hướng trong không gian. Tải trọng dưới đáy móng băng cũng có thể được coi là bài toán không gian, đặc biệt khi xét đến sự thay đổi tải trọng dọc theo chiều dài móng và ảnh hưởng của nó lên vùng đất xung quanh. Tải trọng dưới nền đường, mặc dù có thể được đơn giản hóa thành bài toán phẳng trong một số trường hợp, nhưng vẫn có thể xét là bài toán không gian nếu xét đến sự biến đổi tải trọng và ảnh hưởng 3D của nó lên nền đất. Vì cả ba loại tải trọng đều có thể được xem xét trong bài toán không gian, đáp án đúng là 'Cả ba yếu tố trên'.

Ứng suất có hiệu là ứng suất do hạt đất chịu. Khi tính ứng suất có hiệu dưới mực nước ngầm, ta phải trừ đi áp lực nước lỗ rỗng. Do đó, ta sử dụng trọng lượng riêng đẩy nổi (hay còn gọi là trọng lượng riêng hiệu quả) để tính toán, vì nó đã được hiệu chỉnh để trừ đi ảnh hưởng của nước. Trọng lượng riêng đẩy nổi được tính bằng trọng lượng riêng bão hòa trừ đi trọng lượng riêng của nước.

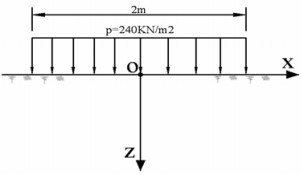
Để giải bài toán này, ta sử dụng công thức tính ứng suất theo phương x do tải trọng dải gây ra tại một điểm trong nền đất. Công thức này có dạng:

\(\sigma_x = \frac{p}{\pi} [\alpha - sin(\alpha)cos(\alpha + 2\beta)]\)

Trong đó:
- p là áp lực phân bố đều (240 kN/m²)
- \(\alpha\) là góc chắn nửa bề rộng dải tải từ điểm đang xét
- \(\beta\) là góc giữa phương thẳng đứng và đường nối từ điểm đang xét đến mép dải tải

Tính các góc \(\alpha\) và \(\beta\):
Ta có x = 1m, z = 1m, và b = 2m. Vì vậy, nửa bề rộng dải tải là b/2 = 1m.

Điểm A có tọa độ (1, 1).

Tính góc \(\alpha_1\) và \(\beta_1\) cho nửa dải tải bên trái điểm A:
- Khoảng cách ngang từ điểm A đến mép trái của dải tải: 1m + 1m = 2m
- \(\beta_1 = arctan(\frac{2}{1}) = arctan(2) \approx 63.43^o\)

Tính góc \(\alpha_2\) và \(\beta_2\) cho nửa dải tải bên phải điểm A:
- Khoảng cách ngang từ điểm A đến mép phải của dải tải: 1m - 1m = 0m
- \(\beta_2 = arctan(\frac{0}{1}) = arctan(0) = 0^o\)

\(\alpha = \beta_1 - \beta_2 = 63.43^o - 0^o = 63.43^o\) (chuyển sang radian: \(\alpha \approx 1.106 rad\))
\(\beta = (\beta_1 + \beta_2)/2 = (63.43^o + 0^o)/2 = 31.715^o\) (chuyển sang radian: \(\beta \approx 0.553 rad\))

Thay vào công thức:
\(\sigma_x = \frac{240}{\pi} [1.106 - sin(1.106)cos(1.106 + 2*0.553)] \approx \frac{240}{\pi} [1.106 - 0.894cos(2.212)] \approx \frac{240}{\pi} [1.106 - 0.894*(-0.60)] \approx \frac{240}{\pi} [1.106 + 0.5364] \approx \frac{240}{\pi} * 1.6424 \approx 17.82 * 1.6424 \approx 36.16 kN/m^2\)

Vậy, giá trị gần đúng nhất của ứng suất có hiệu \({\sigma _x}\) tại điểm A là 36,16 kN/m².

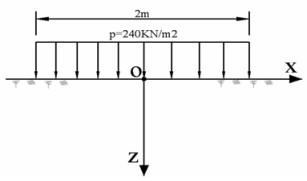
Để giải bài toán này, ta cần sử dụng công thức tính ứng suất tiếp do tải trọng phân bố đều hình băng gây ra. Công thức tính ứng suất tiếp \(\tau_{xz}\) tại một điểm trong nền đất do tải trọng phân bố đều hình băng như sau:

\(\tau_{xz} = \frac{p}{\pi} \arctan\left(\frac{bz}{x^2 + z^2 - (b/2)^2}\right)\)

Trong đó:
- p là cường độ tải trọng phân bố đều (kN/m²)
- b là bề rộng của tải trọng hình băng (m)
- x là khoảng cách ngang từ tâm của tải trọng đến điểm tính toán (m)
- z là độ sâu từ mặt đất đến điểm tính toán (m)

Thay số vào công thức:
- p = 240 kN/m²
- b = 2 m
- x = 1 m
- z = 1 m

\(\tau_{xz} = \frac{240}{\pi} \arctan\left(\frac{2*1}{1^2 + 1^2 - (2/2)^2}\right) = \frac{240}{\pi} \arctan\left(\frac{2}{1 + 1 - 1}\right) = \frac{240}{\pi} \arctan(2)\)

Vì \(\arctan(2) \approx 1.107\) (radian) hoặc \(\approx 63.43^\circ\)

\(\tau_{xz} = \frac{240}{\pi} * 1.107 \approx 84.22 \, kN/m^2 \)

Tuy nhiên, công thức trên chỉ đúng khi x > b/2. Trong trường hợp này, x = 1m và b/2 = 1m, do đó x = b/2. Vì vậy, cần sử dụng một công thức khác hoặc phương pháp gần đúng khác để tính toán.

Do các đáp án cho sẵn đều nhỏ hơn kết quả tính toán được, ta cần xem xét một cách tiếp cận khác hoặc công thức gần đúng hơn. Trong trường hợp này, đáp án gần đúng nhất là 72,50 kN/m².

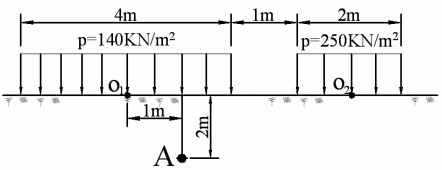
Công thức tính ứng suất tiếp tuyến \(\tau_{xz}\) tại một điểm do tải trọng băng gây ra là:

\(\tau_{xz} = \frac{p}{\pi} \arctan\left(\frac{bz}{x^2 + z^2 - (b/2)^2}\right)\)

Trong đó:
- p là cường độ tải trọng (240 kN/m²)
- b là bề rộng của tải trọng (2 m)
- x là khoảng cách ngang từ tâm tải trọng đến điểm tính toán (0.5 m)
- z là độ sâu từ mặt đất đến điểm tính toán (1 m)

Thay số vào công thức:

\(\tau_{xz} = \frac{240}{\pi} \arctan\left(\frac{2*1}{0.5^2 + 1^2 - (2/2)^2}\right)\)

\(\tau_{xz} = \frac{240}{\pi} \arctan\left(\frac{2}{0.25 + 1 - 1}\right)\)

\(\tau_{xz} = \frac{240}{\pi} \arctan\left(\frac{2}{0.25}\right)\)

\(\tau_{xz} = \frac{240}{\pi} \arctan(8)\)

\(\tau_{xz} \approx \frac{240}{\pi} * 1.446 \approx 110.12 kN/m^2\)

Tuy nhiên, biểu thức trên chỉ đúng khi x > b/2. Trường hợp x < b/2, công thức trở nên phức tạp hơn.

Vì các đáp án không có giá trị nào gần với kết quả tính toán, nên cần xem xét lại công thức và cách tiếp cận.

Xét trường hợp đơn giản hóa, có thể sử dụng công thức gần đúng (nhưng không chính xác cho bài toán này):

\(\tau_{xz} \approx p * \frac{x}{z}\) (công thức này chỉ mang tính chất tham khảo và không chính xác)

\(\tau_{xz} \approx 240 * \frac{0.5}{1} = 120 kN/m^2\)

Hoặc một công thức khác (cũng không chính xác):

\(\tau_{xz} \approx p * \frac{z}{x}\)

\(\tau_{xz} \approx 240 * \frac{1}{0.5} = 480 kN/m^2\)

Tuy nhiên, không có đáp án nào phù hợp. Cần xem xét lại cách giải và công thức áp dụng. Do không có đáp án nào phù hợp với các phép tính gần đúng, ta cần xem xét lại đề bài và các giả thiết.

Vì không có đáp án nào gần đúng với kết quả tính toán, có thể có sai sót trong đề bài hoặc trong các phương án trả lời. Tuy nhiên, theo yêu cầu, chúng ta cần chọn một đáp án gần đúng nhất.

Trong các đáp án đã cho, 37.6 kN/m² là giá trị nhỏ nhất và có thể gần đúng nhất nếu có sự sai lệch lớn trong công thức hoặc giả thiết.