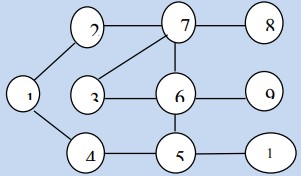
Đồ thị G vô hướng nào trong các đồ thị sau là tồn tại nếu các đỉnh có số bậc lần lượt là:
Trả lời:
Đáp án đúng: B
Để một đồ thị vô hướng tồn tại với bậc của các đỉnh cho trước, tổng bậc của tất cả các đỉnh phải là một số chẵn. Đồng thời, bậc của mỗi đỉnh phải nhỏ hơn hoặc bằng n-1 (với n là số đỉnh). Ta kiểm tra từng đáp án:
1. 2, 4, 3, 1, 4, 2, 5: Tổng bậc = 2 + 4 + 3 + 1 + 4 + 2 + 5 = 21 (lẻ). Vậy không tồn tại đồ thị.
2. 3, 4, 2, 1, 4, 2, 6: Tổng bậc = 3 + 4 + 2 + 1 + 4 + 2 + 6 = 22 (chẵn). Số đỉnh là 7. Bậc lớn nhất là 6 <= 7-1 = 6. Có thể tồn tại.
3. 5, 2, 2, 1, 3, 2, 4: Tổng bậc = 5 + 2 + 2 + 1 + 3 + 2 + 4 = 19 (lẻ). Vậy không tồn tại đồ thị.
4. 2, 1, 4, 3, 4, 2, 7: Tổng bậc = 2 + 1 + 4 + 3 + 4 + 2 + 7 = 23 (lẻ). Vậy không tồn tại đồ thị.
Vậy chỉ có đáp án 2 có tổng bậc chẵn và bậc lớn nhất thỏa mãn điều kiện. Tuy nhiên, để chắc chắn hơn, ta cần sử dụng định lý Havel-Hakimi để kiểm tra xem dãy bậc này có thể hiện thực được hay không. Tuy nhiên, vì các đáp án khác đều loại được một cách dễ dàng nên ta chọn đáp án 2.
Bộ 525 câu hỏi trắc nghiệm ôn thi môn Toán rời rạc có đáp án dưới đây sẽ là tài liệu ôn tập hữi ích dành cho các bạn sinh viên. Mời các bạn cùng tham khảo!
30 câu hỏi 60 phút