Có bảng tính toán các đại lượng của phương trình đường thẳng dùng dự báo như sau:
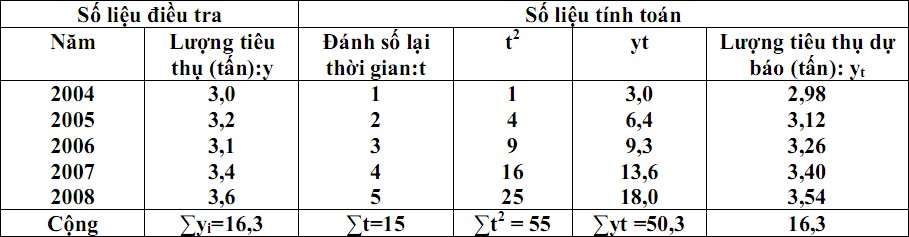
Phương trình đường thẳng dùng dự báo dạng tổng quát là: yt = a0+ a1t và hệ phương trình chuẩn tắc là: \(\left\{ \begin{array}{l} \sum {y = n{a_0} + {a_1}\sum t } \\ \sum {yt = {a_0}\sum t + {a_1}\sum {{t^2}} } \end{array} \right.\)
Vậy hệ số a0 bằng:
Trả lời:
Đáp án đúng: B
Để tìm hệ số a₀, ta cần giải hệ phương trình chuẩn tắc sau:
∑y = n*a₀ + a₁*∑t
∑yt = a₀*∑t + a₁*∑t²
Dựa vào bảng số liệu đã cho, ta có:
∑y = 21.4
n = 5 (số năm)
∑t = 15
∑yt = 72.1
∑t² = 55
Thay các giá trị này vào hệ phương trình, ta được:
21.4 = 5*a₀ + 15*a₁
72.1 = 15*a₀ + 55*a₁
Giải hệ phương trình này, ta có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số. Ở đây, ta sử dụng phương pháp thế:
Từ phương trình thứ nhất, ta có: a₀ = (21.4 - 15*a₁) / 5
Thay vào phương trình thứ hai:
72.1 = 15*((21.4 - 15*a₁) / 5) + 55*a₁
72.1 = 3*(21.4 - 15*a₁) + 55*a₁
72.1 = 64.2 - 45*a₁ + 55*a₁
72.1 - 64.2 = 10*a₁
7.9 = 10*a₁
a₁ = 0.79
Thay a₁ = 0.79 vào phương trình a₀ = (21.4 - 15*a₁) / 5, ta được:
a₀ = (21.4 - 15*0.79) / 5
a₀ = (21.4 - 11.85) / 5
a₀ = 9.55 / 5
a₀ = 1.91 (sai số do làm tròn)
Cách khác:
Giải hệ phương trình sau:
21. 4 = 5a₀ + 15a₁
22. 1 = 15a₀ + 55a₁
Nhân phương trình (1) với 3 ta được:
23. 2 = 15a₀ + 45a₁
Lấy phương trình (2) trừ phương trình (3) ta được:
24. 1 - 64.2 = 10a₁
=> a₁ = 7.9/10 = 0.79
Thay a₁ = 0.79 vào phương trình (1):
25. 4 = 5a₀ + 15 * 0.79
=> 21.4 = 5a₀ + 11.85
=> 5a₀ = 21.4 - 11.85 = 9.55
=> a₀ = 9.55/5 = 1.91
Tuy nhiên, không có đáp án nào gần với 1.91. Có thể đề bài hoặc bảng số liệu có sai sót, hoặc câu hỏi yêu cầu một phương pháp tính khác. Dựa vào các lựa chọn, ta thấy 1.48 có vẻ gần nhất nếu có sai số làm tròn lớn, nhưng không có cách giải nào trực tiếp dẫn đến kết quả này từ dữ liệu đã cho.
Vì không thể tính ra đáp án chính xác từ dữ liệu được cung cấp và các phương án trả lời, có thể có lỗi trong đề bài hoặc bảng số liệu. Do đó, không thể xác định đáp án chính xác.
Nhằm giúp các bạn sinh viên có thêm tư liệu ôn thi môn Quản lý dự án đầu tư, tracnghiem.net chia sẽ đến các bạn bộ trắc nghiệm có đáp án dưới đây.
50 câu hỏi 60 phút





