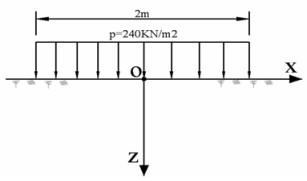
Cho một tải trọng hình băng phân bố đều trên mặt đất với bề rộng b = 2m, tải trọng p = 240kN/m2 như hình vẽ. Hãy xác định giá trị gần đúng nhất ứng suất có hiệu \({\sigma _x}\) tại điểm A(x = 0.5m; z = 1m) do tải trọng gây ra:

Đáp án đúng: C

Để giải bài toán này, ta sử dụng công thức tính ứng suất theo phương x do tải trọng phân bố đều hình băng gây ra: \(\sigma_x = \frac{p}{\pi} [\alpha - \sin(\alpha) \cos(2\beta)]\) Trong đó: * \(p\) là cường độ tải trọng phân bố đều, \(p = 240\) kN/m². * \(\alpha\) là góc chắn dải tải trọng nhìn từ điểm A. * \(\beta\) là góc hợp bởi đường thẳng nối điểm A với trung điểm của dải tải trọng và phương thẳng đứng. Tính các góc \(\alpha\) và \(\beta\): * \(x_1 = x + \frac{b}{2} = 0.5 + \frac{2}{2} = 1.5\) m * \(x_2 = -x + \frac{b}{2} = -0.5 + \frac{2}{2} = 0.5\) m * \(\alpha = arctan(\frac{x_1}{z}) + arctan(\frac{x_2}{z}) = arctan(\frac{1.5}{1}) + arctan(\frac{0.5}{1}) = arctan(1.5) + arctan(0.5) \approx 56.31^\circ + 26.57^\circ = 82.88^\circ = 1.445 rad\) * \(\beta = \frac{arctan(\frac{x_1}{z}) - arctan(\frac{x_2}{z})}{2} = \frac{arctan(1.5) - arctan(0.5)}{2} = \frac{56.31^\circ - 26.57^\circ}{2} = \frac{29.74^\circ}{2} = 14.87^\circ = 0.259 rad\) Thay các giá trị vào công thức tính \(\sigma_x\): \(\sigma_x = \frac{240}{\pi} [1.445 - \sin(1.445) \cos(2*0.259)] = \frac{240}{\pi} [1.445 - \sin(82.88^\circ) \cos(29.74^\circ)] = \frac{240}{\pi} [1.445 - 0.992 * 0.868] = \frac{240}{\pi} [1.445 - 0.861] = \frac{240}{\pi} * 0.584 \approx 44.49\) kN/m² Giá trị gần đúng nhất là 44,7 kN/m².

p(kN/m²)	100	200	300	400
e	0,665	0,625	0,605	0,592

Cho một tải trọng hình băng phân bố đều trên mặt đất với bề rộng b = 2m, tải trọng p = 240kN/m² như hình vẽ. Hãy xác định giá trị gần đúng nhất ứng suất có hiệu \({\sigma _x}\) tại điểm A(x = 0.5m; z = 1m) do tải trọng gây ra:

300+ Câu trắc nghiệm môn Cơ học đất có đáp án - Phần 4

Câu hỏi liên quan

Bộ Đồ Án Tốt Nghiệp Ngành Trí Tuệ Nhân Tạo Và Học Máy

Bộ 120+ Đồ Án Tốt Nghiệp Ngành Hệ Thống Thông Tin

Bộ Đồ Án Tốt Nghiệp Ngành Mạng Máy Tính Và Truyền Thông

Bộ Luận Văn Tốt Nghiệp Ngành Kiểm Toán

Bộ 370+ Luận Văn Tốt Nghiệp Ngành Kế Toán Doanh Nghiệp

Bộ Luận Văn Tốt Nghiệp Ngành Quản Trị Thương Hiệu

ĐĂNG KÝ GÓI THI VIP