Tuyển Tập Đề Thi Tham Khảo Tốt Nghiệp THPT Quốc Gia Năm 2025 - Toán - Bộ Đề 04 - Đề Số 01
Câu 1
Cho hình chóp \(S.ABC\) có đường thẳng \(SA\) vuông góc với đáy \(\left( ABC \right)\), \(SA=2a\). Khoảng cách từ điểm \(S\) đến đường thẳng \(AB\) bằng:
A.\(a.\)
B.\(3a.\)
C.\(2a.\)
D.\(\frac{a}{2}.\)
Câu 2
Cho hàm số \(y=f\left( x \right)\) xác định trên \(\mathbb{R}\) thỏa mãn \(\underset{x\to 2}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 2 \right)}{x-2}=3\).
Kết quả đúng là:
A.\({f}'\left( 2 \right)=3\).
B.\({f}'\left( x \right)=2\).
C.\({f}'\left( x \right)=3\).
D.\({f}'\left( 3 \right)=2\).
Câu 3
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình bên. Giá trị nhỏ nhất của hàm số \(y=f\left( x \right)\) trên \(\left[ -1\,;\,1 \right]\) bằng:
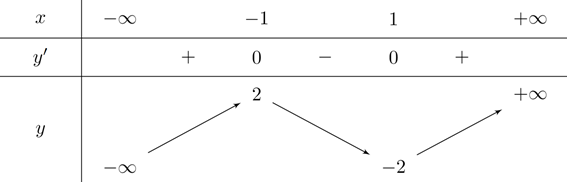 A.
A.\(-3\).
B.\(-1\).
C.\(-2\).
D.\(1\).
Câu 4
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(B\). Đường thẳng \(SA\) vuông góc với đáy \(ABC\). Đường thẳng \(BC\) vuông góc với mặt phẳng nào sau đây?
A.\(\left( SAC \right)\).
B.\(\left( SBC \right)\).
C.\(\left( ABC \right)\).
D.\(\left( SAB \right)\).
Câu 5
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(a.\) Khoảng cách từ \({A}'\) đến mp \((ABCD)\) bằng:
A.\(\frac{a}{2}.\)
B.\(a.\)
C.\(2a.\)
D.\(3a.\)
Câu 6
Một nhóm học sinh gồm \(20\) học sinh nam và \(10\) học sinh nữ. Có bao nhiêu cách chọn một học sinh trong nhóm đó tham gia đội thanh niên tình nguyện của trường?
A.\(200\).
B.\(20\).
C.\(30\).
D.\(10\).
Câu 7
Cho hàm số bậc ba \(y=f\left( x \right)\) có đồ thị là đường cong hình bên.
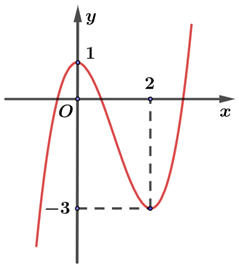
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.\(\left( -\infty ;0 \right)\).
B.\(\left( 2;+\infty \right)\).
C.\(\left( -3;1 \right)\).
D.\(\left( 0;2 \right)\).
Câu 8
Cho hình chóp tam giác đều \(S.ABC\). Mặt bên \(SBC\) là tam giác gì?
A.Đều.
B.Vuông.
C.Vuông cân.
D.Cân.
Câu 9
Một vật chuyển động có phương trình \(s\left( t \right)=3\cos t\). Khi đó, vận tốc tức thời tại thời điểm \(t\) của vật là:
A.\(v\left( t \right)=-3\sin t\).
B.\(v\left( t \right)=-3\cos t\).
C.\(v\left( t \right)=3\cos t\).
D.\(v\left( t \right)=3\sin t.\)
Câu 10
Nghiệm của phương trình \(\cos x=\cos \frac{\pi }{4}\) là:
A.\(x=-\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}.\)
B.\(x=\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}.\)
C.\(x=\pm \frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}.\)
D.\(x=\pm \frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}.\)
Câu 11
Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ -2;2 \right]\) và có đồ thị là đường cong trong hình bên dưới.
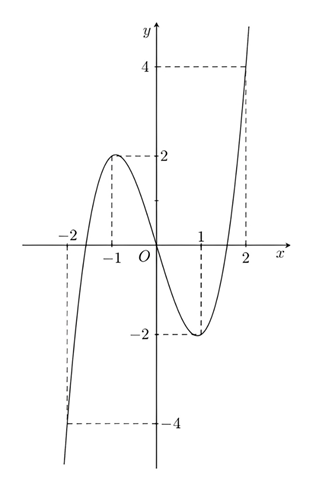
Hàm số \(y=f\left( x \right)\) đạt cực tiểu tại điểm:
A.\(x=-2\).
B.\(x=-1\).
C.\(x=1\).
D.\(x=0\).
Câu 12
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Mốt của mẫu số liệu trên là:
A.\(52\).
B.\(42\).
C.\(53\).
D.\(54\).
Câu 13
Một bệnh nhân hàng ngày phải uống \(150mg\) thuốc kháng sinh đặc trị bệnh bạch hầu. Sau một ngày hàm lượng thuốc kháng sinh đặc trị bệnh bạch hầu trong cơ thể vẫn còn \(6%\) lượng thuốc của ngày hôm trước.
Các mệnh đề sau đúng hay sai?
a) Lượng thuốc kháng sinh đặc trị bệnh bạch hầu còn trong cơ thể sau ngày đầu tiên uống thuốc là \(9(mg)\).
b) Lượng thuốc kháng sinh đặc trị bệnh bạch hầu có trong cơ thể sau khi uống viên thuốc của ngày thứ \(2\) là \(159(mg)\).
c) Lượng thuốc kháng sinh đặc trị bệnh bạch hầu có trong cơ thể sau khi uống viên thuốc của ngày thứ \(4\) là \(170(mg)\).
d) Ước tính lượng thuốc kháng sinh đặc trị bệnh bạch hầu trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian 30 ngày là \(159,57mg\).
Câu 14
Cho \(x,y\) là các số thực thỏa mãn \(f(x,y)={{\log }_{4}}\left( x+y \right)+{{\log }_{4}}\left( x-y \right)\ge 1\,\,(*)\).
Các khẳng định sau đúng hay sai?
a) Điều kiện xác định của hàm số \(f(x,y)\) là \(\left\{ \begin{align} & x+y>0 \\ & x-y>0 \\ \end{align} \right.\).
b) Với cặp số \(x,y\) thỏa mãn điều kiện xác định của hàm số \(f(x,y)\), ta có: \(f(x,y)={{x}^{2}}-{{y}^{2}}\).
c) Cặp số \(\left\{ \begin{align} & x=8 \\ & y=16 \\ \end{align} \right.\) thỏa mãn \(f(x,y)={{\log }_{4}}\left( x+y \right)+{{\log }_{4}}\left( x-y \right)\ge 1\).
d) Với \(P=2x-y\) thì \({{P}_{\min }}=2\sqrt{3}\).
Câu 15
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\,\bot \,\left( ABCD \right)\), biết \(SC=a\sqrt{3}\). Gọi M, N, P, Q lần lượt là trung điểm của \(SB\), \(SD\), \(CD\), \(BC\). Các mệnh đề sau đúng hay sai?
a) Thể tích của khối chóp \(S.ABCD\) bằng \(\frac{1}{3}SA.{{S}_{ABCD}}\).
b) Thể tích của khối chóp \(S.ABC\) bằng thể tích của khối chóp \(S.ACD\).
c) Thể tích của khối chóp \(S.ABCD\) bằng \({{a}^{3}}\).
d) Thể tích của khối chóp \(A.MNPQ\) bằng \(\frac{{{a}^{3}}}{8}\).
Câu 16
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ
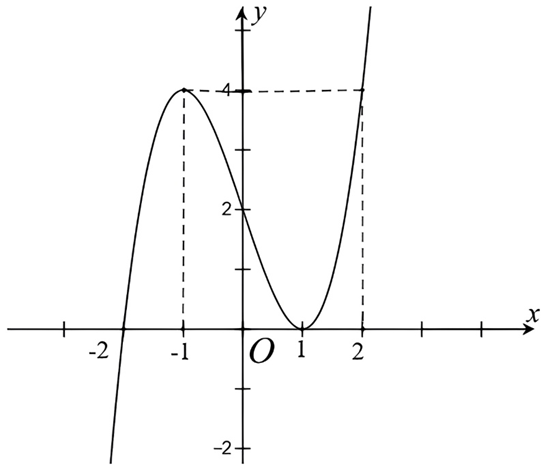
Các mệnh đề sau đây đúng hay sai?
a) Hàm số nghịch biến trên khoảng \(\left( -1;1 \right)\).
b) Hàm số có \({f}'\left( x \right)>0\) \(\forall x\in \left( -\infty ;-1 \right)\cup \left( 1;+\infty \right)\).
c) Hàm số \(g\left( x \right)=f\left( x \right)+1\) nghịch biến trên khoàng \(\left( 0;2 \right)\).
d) Hàm số \(y=f\left( \left| x \right| \right)\) đồng biến trên \(\left( -1;0 \right)\) và \(\left( 1;+\infty \right)\).
Top 10/0 lượt thi
| Tên | Điểm | Thời gian |
|---|















