Bộ Đề Kiểm Tra Tham Khảo Học Kì II - Toán 11 - Kết Nối Tri Thức Với Cuộc Sống – Bộ Đề 01 - Đề Số 01
Câu 1
Rút gọn biểu thức \(P = x^{\frac{1}{3}} \cdot \sqrt[6]{x}\) với \(x > 0\).
A.\(P = \sqrt{x}\).
B.\(P = x^{\frac{5}{6}}\).
C.\(P = x^{2}\).
D.\(P = x^{\frac{2}{3}}\).
Câu 2
Hàm số \(y = \log_{5} (4x-x^{2})\) có tập xác định là:
A.\(\mathscr{{D}} = (0;4)\).
B.\(\mathscr{{D}} = \mathbb{{R}}\).
C.\(\mathscr{{D}} = (-\infty;0) \cup (4;+\infty)\).
D.\(\mathscr{{D}} = (0;+\infty)\).
Câu 3
Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai đường thẳng \(BA'\) và \(CD\) bằng:
A.\(45^\circ\).
B.\(60^\circ\).
C.\(30^\circ\).
D.\(90^\circ\).
Câu 4
Cho hình chóp \(S.ABC\) có \(SA \perp (ABC)\); tam giác \(ABC\) đều cạnh \(a\) và \(SA = a\) (tham khảo hình vẽ bên). Tìm góc giữa đường thẳng \(SC\) và mặt phẳng \((ABC)\).
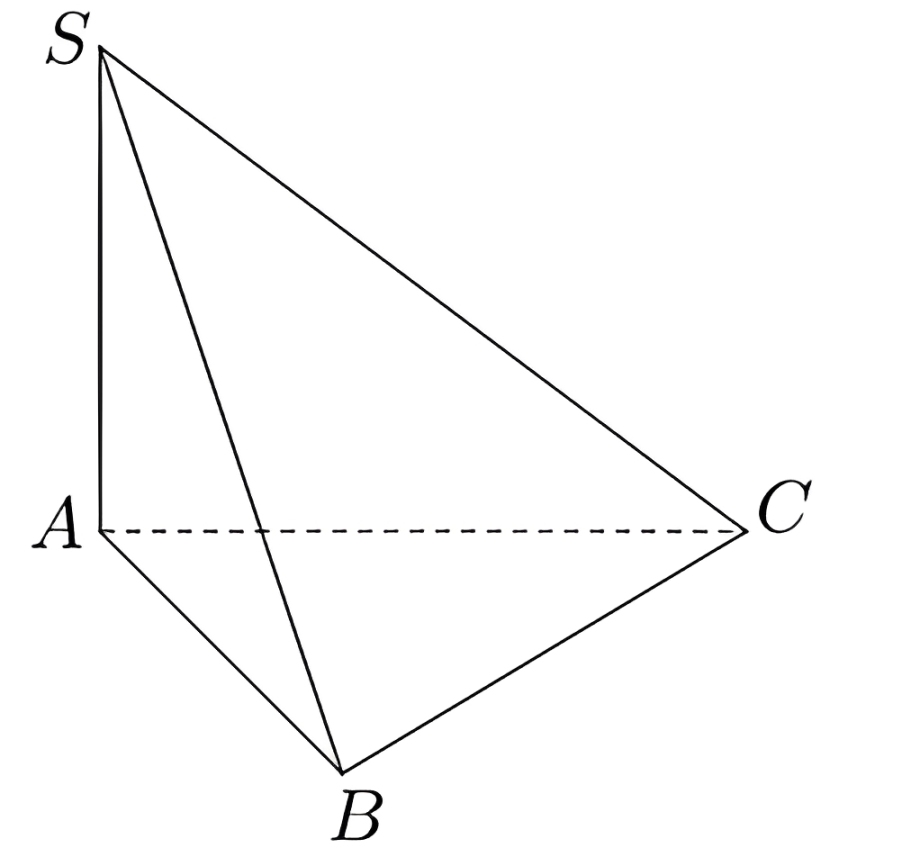 A.
A.\(60^\circ\).
B.\(45^\circ\).
C.\(135^\circ\).
D.\(90^\circ\).
Câu 5
Cho hình lập phương \(ABCD.A'BC'D'\). Tính góc giữa mặt phẳng \((ABCD)\) và \((ACC'A')\).
A.\(45^\circ\).
B.\(60^\circ\).
C.\(30^\circ\).
D.\(90^\circ\).
Câu 6
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, cạnh bên \(SA\) vuông góc với đáy. Biết khoảng cách từ \(A\) đến \((SBD)\) bằng \(\frac{6a}{7}\). Tính khoảng cách từ \(C\) đến mặt phẳng \((SBD)\)?
A.\(\frac{12a}{7}\).
B.\(\frac{3a}{7}\).
C.\(\frac{4a}{7}\).
D.\(\frac{6a}{7}\).
Câu 7
Cho khối tứ diện \(ABCD\) có \(AB, AC, AD\) đôi một vuông góc và \(AB = AC = 2a\), \(AD = 3a\). Thể tích \(V\) của khối tứ diện đó là:
A.\(V = a^{3}\).
B.\(V = 3a^{3}\).
C.\(V = 2a^{3}\).
D.\(V = 4a^{3}\).
Câu 8
Trên giá sách có các quyển vở không nhãn xếp cạnh nhau với bề ngoài, khối lượng và kích thước giống hệt nhau, trong đó có 5 quyển ghi môn Toán, 5 quyển ghi môn Ngữ Văn và 3 quyển ghi môn Tiếng Anh. Lấy ngẫu nhiên hai quyển vở. Xét các biến cố:
M: "Trong hai quyển vở được lấy, chỉ có 1 quyển ghi môn Tiếng Anh";
N: "Trong hai quyển vở được lấy, chỉ có 1 quyển ghi môn Ngữ Văn".
Khi đó, biến cố giao của hai biến cố \(M\) và \(N\) là:
A."Hai quyển vở được lấy ghi cùng một môn".
B."Hai quyển vở được lấy ghi hai môn khác nhau".
C."Trong hai quyển vở được lấy, một quyển ghi môn Tiếng Anh và một quyển ghi môn Ngữ Văn".
D."Hai quyển vở được lấy có ít nhất một quyển ghi môn Tiếng Anh”.
Câu 9
Một hộp đựng 4 viên bi đỏ, 3 viên bi xanh, 2 viên bi vàng. Chọn ngẫu nhiên 2 viên bi. Tính xác suất 2 viên bị được chọn cùng màu là:
A.\(P(X)=\frac{5}{18}\).
B.\(P(X) = \frac{5}{8}\).
C.\(P(X) = \frac{7}{18}\).
D.\(P(X)=\frac{7}{8}\).
Câu 10
Có hai hộp đựng bi. Hộp có 9 viên bị được đánh số 1,2,3....., 9. Lấy ngẫu nhiên mỗi hộp một viên bi. Biết rằng xác suất để lấy được viên bị mang số chẵn ở hộp II là \(\frac{3}{10}\). Xác suất để lấy được cả hai viên bị mang số chẵn là:
A.\(P = \frac{2}{18}\).
B.\(P = \frac{2}{19}\).
C.\(P = \frac{5}{18}\).
D.\(P = \frac{2}{15}\).
Câu 11
Đạo hàm của hàm số \(y = \ln(1-x^{2})\) là:
A.\(\frac{2x}{x^{2}-1}\).
B.\(\frac{-2x}{x^{2}-1}\).
C.\(\frac{1}{x^{2}-1}\).
D.\(\frac{x}{1-x^{2}}\).
Câu 12
Cho chuyển động thẳng xác định bởi phương trình \(S = -t^{3} + 3t^{2} +9t\), trong đó \(t\) tính bằng giây và \(S\) tính bằng mét. Tính vận tốc của chuyển động tại thời điểm gia tốc triệt tiêu.
A.\(12m/s\).
B.\(0m/s\).
C.\(11m/s\).
D.\(6m/s\).
Câu 13
Một trường học có tỉ lệ học sinh nam và nữ là 5:3. Trong đó, tỉ lệ số học sinh nam thuận tay trái là \(11\%\), tỉ lệ số học sinh nữ thuận tay trái là \(9\%\). Khi đó:
Xác suất để chọn được 1 học sinh nam ở trường không thuận tay trái là: \(\frac{273}{800}\).
Xác suất để chọn được 1 học sinh nữ ở trường không thuận tay trái là: \(\frac{89}{160}\).
Xác suất để chọn được 1 học sinh nam, 1 học sinh nữ ở trường thuận tay trái lần lượt là: \(\frac{11}{160}\) và \(\frac{27}{800}\)
Xác suất để chọn ngẫu nhiên 5 học sinh ở trường trong đó có đúng 1 học sinh nam và 1 học sinh nữ thuận tay trái là: \(\frac{297}{128000}\).
Câu 14
Cho hàm số \(f(x) = 3^{2x} -2.3^{x}\) có đồ thị như hình vẽ sau:
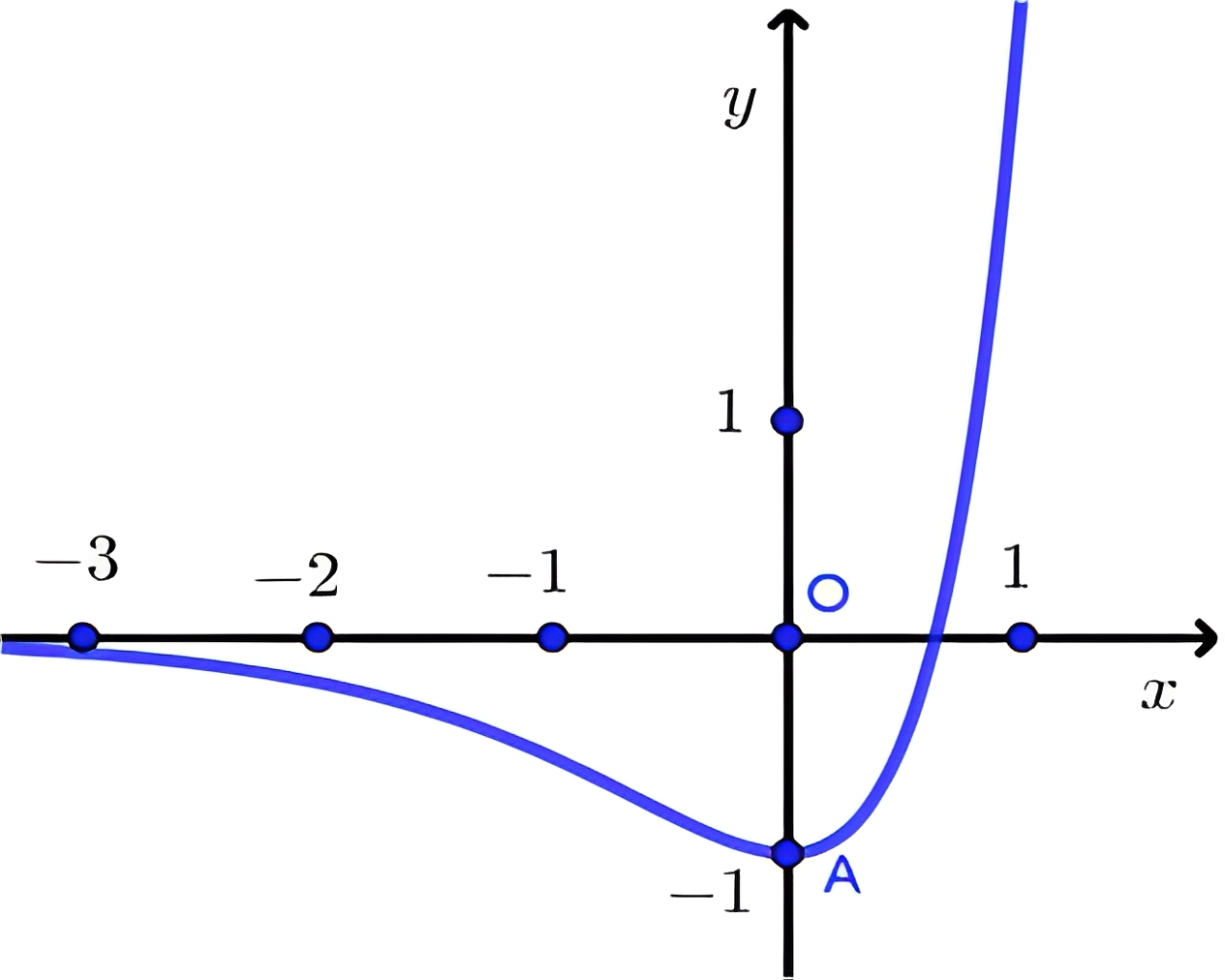
Đường thẳng \(y = 0\) cắt đồ thị hàm số \((C)\) tại điểm có hoành độ là \(x = \log_{3} 2\).
Bất phương trình \(f (x) \geqslant -1\) có nghiệm duy nhất.
Bất phương trình \(f(x) \geqslant 0\) có tập nghiệm là: \((-\infty;\log_{3} 2)\).
Đường thẳng \(y = 0\) cắt đồ thị hàm số \((C)\) tại 2 điểm phân biệt.
Top 10/0 lượt thi
| Tên | Điểm | Thời gian |
|---|















