Trong các số đặc trưng đo xu thế trung tâm dưới đây, số nào thỏa mãn có \(75\%\) giá trị trong mẫu số liệu nhỏ hơn nó và \(25\%\) giá trị trong mẫu số liệu lớn hơn nó?

Điều tra về số lượng học sinh khối 11 trong một lớp học, người ta thu được dữ liệu của 100 lớp học và có bảng phân phối tần số ghép nhóm sau:

\(\begin{array}{|l|c|c|c|c|c|} \hline \text { Nhóm } & {[36 ; 38)} & {[38 ; 40)} & {[40 ; 42)} & {[42 ; 44)} & {[44 ; 46)} \\ \hline \text { Tần số } & 9 & 15 & 25 & 30 & 21 \\ \hline \end{array}\)

Tìm trung vị của mẫu số liệu ghép nhóm trên. (làm tròn đến số thập phân thứ hai)

Thời gian (phút) di chuyển đến trường của nhóm học sinh trường THPT \(A\) được tổng hợp dưới bảng sau:

\[\begin{array}{|c|c|} \hline \text { Thời gian (phút) } & \text { Số học sinh } \\ \hline[15 ; 20) & 6 \\ \hline[20 ; 25) & 14 \\ \hline[25 ; 30) & 25 \\ \hline[30 ; 35) & 37 \\ \hline[35 ; 40) & 13 \\ \hline[40 ; 45) & 9 \\ \hline[45 ; 50) & 21 \\ \hline \end{array}\]

Tìm trung vị của mẫu số liệu ghép nhóm trên? (làm tròn đến hàng phần mười).

Khảo sát thời gian chơi thể thao trong một ngày của một số học sinh khối11, thu được mẫu số liệu ghép nhóm sau:

\[\begin{array}{|c|c|} \hline \mathbf{\text { Thời gian (phút) }} & \mathbf{\text { Số học sinh }} \\ \hline[0 ; 20) & 9 \\ \hline[20 ; 40) & 5 \\ \hline[40 ; 60) & 12 \\ \hline[60 ; 80) & 6 \\ \hline[80 ; 100) & 10 \\ \hline \end{array}\]

Tính thời gian chơi thể thao trung bình trong một ngày của các học sinh này.

Người ta đo đường kính của 61 cây gỗ được trồng sau 12 năm(đơn vị: centimét), họ thu được bảng tần số ghép nhóm sau:

\(\begin{array}{|c|c|c|c|c|c|} \hline \text { Đường kính } & {[20 ; 25)} & {[25 ; 30)} & {[30 ; 35)} & {[35 ; 40)} & {[40 ; 45)} \\ \hline \text { Số cây } & 4 & 12 & 26 & 13 & 6 \\ \hline \end{array}\)

Thống kê điểm thi đánh giá năng lực của một trường THPT qua thang điểm 100 được cho ở bảng sau:

Trung vị của mẫu số liệu ghép nhóm thuộc khoảng nào sau đây?

Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Tính \(9{{Q}_{1}}-{{Q}_{3}}\).

Kết quả đo chiều cao của 250 cây dừa đột biến 3 năm tuổi ở một viện nghiên cứu được tổng hợp ở bảng sau:

\(\begin{array}{|c|c|c|c|c|c|} \hline \begin{array}{c} \text { Chiều cao } \\ \left(m^2\right) \end{array} & {[8,5 ; 8,8)} & {[8,8 ; 9,1)} & {[9,1 ; 9,4)} & {[9,4 ; 9,7)} & {[9,7 ; 10)} \\ \hline \begin{array}{c} \text { Giá trị } \\ \text { đại diện } \end{array} & 8,65 & 8,95 & 9,25 & 9,55 & 9,85 \\ \hline \end{array}\)

Tìm cân nặng trung bình của học sinh lớp 11 đó.

Cho mẫu số liệu điểm môn Toán của một nhóm học sinh như sau: 

 Mốt của mẫu số liệu (kết quả làm tròn đến hàng phần trăm) là:

Cho mẫu số liệu ghép nhóm sau:

\[\begin{array}{|c|c|c|c|c|} \hline \mathbf{\text { Nhóm }} & {[1 ; 5)} & {[5 ; 9)} & {[9 ; 13)} & {[13 ; 17)} \\ \hline \mathbf{\text { Tần số }} & 5 & 8 & 11 & 6 \\ \hline \end{array}\]

Nhóm chứa mốt của mẫu số liệu ghép nhóm trên là:

Điểm thi môn Toán (thang điểm 100) của 60 thí sinh được cho trong bảng sau:

Có bao nhiêu học sinh thi trượt môn Toán? Biết rằng thí sinh đạt từ 50 điểm trở nên thì tính là đỗ.

Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

\[\begin{array}{|c|c|} \hline \mathbf{\text { Doanh thu }} & \mathbf{\text { Số ngày }} \\ \hline[5 ; 7) & 2 \\ \hline[7 ; 9) & 7 \\ \hline[9 ; 11) & 7 \\ \hline[11 ; 13) & 3 \\ \hline[13 ; 15) & 1 \\ \hline \end{array}\]

Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?

Bảng dưới biểu thị kết quả điều tra thời gian sử dụng Internet hằng ngày của một số người.

Mốt của bảng số liệu trên thuộc nhóm nào?

Cho mẫu số liệu ghép nhóm có bảng tần số ghép nhóm như sau:

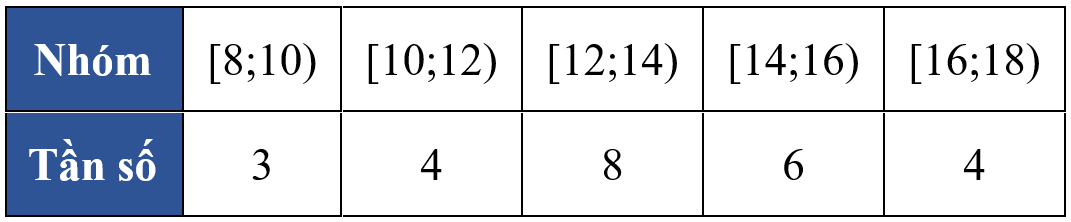
Trung vị của bảng số liệu trên thuộc nhóm nào?

Khảo sát về thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:

\[\begin{array}{|c|c|} \hline \mathbf{\text { Thời gian (giờ) }} & \mathbf{\text { Số học sinh }} \\ \hline[0 ; 4) & 3 \\ \hline[4 ; 8) & 15 \\ \hline[8 ; 12) & 10 \\ \hline[12 ; 16) & 8 \\ \hline[16 ; 20) & 4 \\ \hline \end{array}\]

Thời gian xem tivi trung bình trong tuần trước của các bạn học sinh này là

Một công ty bất động sản Đất Vàng thực hiện cuộc khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào để tiến hành dự án xây nhà ở Thăng Long group sắp tới. Kết quả khảo sát \(500\) khách hàng được ghi lại ở bảng sau:

\(\begin{array}{|c|c|} \hline \text { Múc giá (triệu đồng/m²) } & \text { Số khách hàng } \\ \hline[10 ; 14) & 75 \\ \hline[14 ; 18) & 104 \\ \hline[18 ; 22) & 179 \\ \hline[22 ; 26) & 96 \\ \hline[26 ; 30) & 45 \\ \hline \end{array}\)

Công ty bất động sản Đất Vàng nên xây nhà ở mức giá bao nhiêu triệu đồng để nhiều người có nhu cầu xây nhà? (ghi kết quả dưới dạng số thập phân)

Một bưu tá thống kê lại số bưu phẩm gửi đến một cơ quan mỗi ngày trong tháng 6/2022 trong bảng sau:

\[\begin{array}{|c|c|c|c|c|c|} \hline \mathbf{\text { Số bưu phẩm }} & {[20 ; 24]} & {[25 ; 29]} & {[30 ; 34]} & {[35 ; 39]} & {[40 ; 44]} \\ \hline \mathbf{\text { Số ngày }} & 4 & 6 & 10 & 6 & 4 \\ \hline \end{array}\]

Số trung bình của mấu số liệu là

Cô Hà thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Nhóm chứa tứ phân vị thứ nhất có tần số bằng bao nhiêu?

Đo chiều cao (tính bằng cm) của 300 học sinh một trường THCS thu được kết quả như sau:

Tần số tích lũy của nhóm \([154 ; 158)\) là:

Thời gian (phút) xem tivi mỗi buổi tối của một số học sinh được cho trong bảng sau:

\[\begin{array}{|c|c|} \hline \mathbf{\text { Thò̀ gian (phút) }} & \mathbf{\text { Số học sinh }} \\ \hline[6,5 ; 9,5) & 2 \\ \hline[9,5 ; 12,5) & 3 \\ \hline[12,5 ; 15,5) & 12 \\ \hline[15,5 ; 18,5) & 15 \\ \hline[18,5 ; 21,5) & 24 \\ \hline[21,5 ; 24,5) & 2 \\ \hline[24,5 ; 27,5) & 2 \\ \hline \end{array}\]

Số trung vị của mẫu số liệu ghép nhóm này là