Hạt nhân \(_{92}^{235}U\) có năng lượng liên kết 1784 MeV. Năng lượng liên kết riêng của hạt nhân này là
"Bộ Đề Kiểm Tra Học Kì II - Vật Lí 12 - Cánh Diều - Bộ Đề 01" là tài liệu ôn tập được biên soạn dành cho học sinh lớp 12, giúp các em hệ thống hóa kiến thức trọng tâm và luyện tập kỹ năng làm bài kiểm tra học kỳ II theo chương trình sách giáo khoa Chân Trời Sáng Tạo. Tài liệu đi kèm đáp án chi tiết, hỗ trợ học sinh trong quá trình tự học, tự ôn luyện, đồng thời giúp giáo viên có thêm nguồn tài liệu tham khảo tin cậy trong công tác kiểm tra đánh giá cuối học kỳ.
Câu hỏi liên quan
Độ hụt khối của một hạt nhân bằng
Hạt nhân \({}_{{\text{92}}}^{{\text{235}}}{\text{U}}\) có năng lượng liên kết 1784 MeV. Năng lượng liên kết riêng của hạt nhân này là
Xét đồng vị không bền của nickel là \({}_{28}^{66}\text{Ni}\) phát ra tia phóng xạ \({{\text{ }\!\!\beta\!\!\text{ }}^{-}}\) và biến thành hạt nhân con \({}_{29}^{66}\text{Cu}\). Biết rằng khối lượng của các hạt nhân trên lần lượt là \({{\text{m}}_{\text{Ni}}}\) = 65,9297 amu và \({{\text{m}}_{\text{Cu}}}\) = 65,9289 amu; khối lượng của electron là 0,0006 amu. Năng lượng toả ra của quá trình phóng xạ được xác định bởi biểu thức DE = (\({{\text{m}}_{\text{tt}}}\) – \({{\text{m}}_{\text{sp}}}\))\({{\text{c}}^{2}}\) với \({{\text{m}}_{\text{tt}}}\) và \({{\text{m}}_{\text{sp}}}\) lần lượt là tổng khối lượng của các hạt trước và sau phản ứng.
Lấy 1 uc2 = 931,5 MeV. Năng lượng tỏa ra của quá trình phóng xạ trên bằng bao nhiêu MeV (làm tròn kết quả đến hàng phần trăm)?
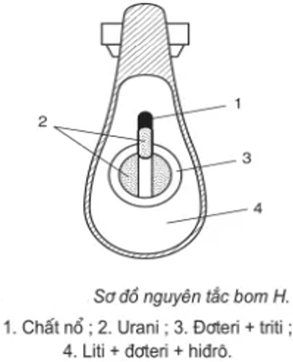
Bom hydrogen (bom H) là một loại vũ khí hạt nhân có sức tàn phá lớn hơn bom nguyên tử (bom A) rất nhiều lần, dù hiện nay cả bom hydrogen và bom nguyên tử đều không được sử dụng trong các cuộc chiến tranh. Sở dĩ bom hydrogen có sức tàn phá lớn như vậy là do nó là sự kết hợp của phản ứng phân hạch của \({}_{92}^{235}U\) (giai đoạn 1) để tạo ra môi trường có nhiệt độ rất cao, cung cấp động năng cho các hạt tham gia phản ứng nhiệt hạch (giai đoạn 2) theo phương trình phản ứng: \({}_{1}^{2}H+{}_{1}^{3}H\to {}_{2}^{4}He+{}_{0}^{1}n+17,6\text{ }MeV\).Giả sử năng lượng toả ra từ quá trình phân hạch còn lại sau khi tạo phản ứng nhiệt hạch là 2,8.1010 J và khối lượng \({}_{2}^{4}He\) được tạo thành từ một vụ nổ bom hydrogen trong thí nghiệm vũ khí hạt nhân là 200 g.
Cho số Avogadro là \({{N}_{A}}=6,{{022.10}^{23}}mo{{l}^{-1}}\). Biết \(1\text{ }eV=1,{{6.10}^{-19}}J\).Biết khối lượng của proton là 1,00728 amu; của neutron là 1,00866 amu; của hạt nhân \({}_{11}^{23}\text{Na}\) là 22,98373 amu và 1 amu = 931,5 MeV/c2. Năng lượng liên kết của \({}_{11}^{23}\text{Na}\) bằng bao nhiêu MeV (làm tròn kết quả đến hàng đơn vị) ?
Hạt nhân càng bền vững nếu nó có
Cho biết khối lượng nguyên tử của các hạt \(_{1}^{1}H\); \(_{15}^{31}P\); \(_{16}^{32}S\). ; \(_{17}^{33}Cl\) l lượt là 1,00783u; 30,97376u; 31,97207u; 32,97745u; hạt neutron có khối lượng 1,0087u và hạt proton có khối lượng 1,0073u.
Khối lượng của các hạt proton, neutron và hạt nhân \(_{8}^{18}O\) lần lượt là 1,0073 amu; 1,0087 amu; 17,9948 amu. Biết 1 amu = 931,5 MeV/c2.
Độ hụt khối của hạt nhân \(_{8}^{18}O\) là bao nhiêu amu (làm tròn kết quả đến chữ số hàng phần trăm)?
Một hạt nhân có 8 proton và 9 neutron. Năng lượng liên kết riêng của hạt nhân này bằng 7,75 MeV/nucleon. Biết khối lượng của proton và neutron lần lượt là 1,0073 amu và 1,0087 amu. Lấy \(1~\text{amu}=931,5~\text{MeV}/{{\text{c}}^{2}}\). Khối lượng của hạt nhân này bằng
Năng lượng của Mặt Trời và các ngôi sao trong vũ trụ đều có nguồn gốc từ các phản ứng nhiệt hạch, bắt đầu từ việc đốt cháy hydrogen để tạo thành helium (được gọi là chu trình proton – proton). Xét một ngôi sao đã đốt cháy hoàn toàn hydrogen thành helium và coi rằng các hạt nhân helium tạo thành đều tham gia vào quá trình ba – alpha theo phương trình: 3.\({}_{2}^{4}\text{He}\) \({}_{6}^{12}\text{C}\) + 7,275 MeV. Nếu khối lượng của ngôi sao vào thời điểm đó là 4.1030 kg (khi tất cả hạt nhân trong ngôi sao đều là helium) và công suất tỏa nhiệt của ngôi sao là 3,8.1030 W thì sau bao nhiêu triệu năm toàn bộ hạt nhân \({}_{2}^{4}\text{He}\) sẽ chuyển hóa hoàn toàn thành \({}_{6}^{12}\text{C}\)? Lấy khối lượng nguyên tử \({}_{2}^{4}\text{He}\) bằng 4 amu và một năm có 365 ngày.
Một quả bom sử dụng năng lượng từ các phản ứng nhiệt hạch để nén nguồn nhiên liệu nhằm tăng sức công phá lên hàng chục, hàng trăm lần. Nhiên liệu tổng hợp cho phản ứng nhiệt hạch này là hạt nhân Đoteri (\({}_{1}^{2}H\)), diễn ra theo phương trình: \(5_{1}^{2}\text{H}\to _{2}^{3}\text{He}+_{2}^{4}\text{He}+_{1}^{1}\text{H}+2\text{n}\). Lấy khối lượng các hạt \({}_{1}^{1}H,{}_{1}^{2}H,~{}_{2}^{3}He,{}_{2}^{4}He\) và notron lần lượt là 1,0079u; 2,0141u; 3,0160u; 4,0026u và 1,0087u. Cho 1uc2 = 931,5MeV, số A-vô-ga-rô là \({{N}_{A}}={{6,02.10}^{23}}\text{mo}{{\text{l}}^{-1}}\). Quả bom đó có 150kg Đoteri tham gia thực hiện phản ứng tổng hợp,năng lượng tỏa ra từ quả bom là:
Cho khối lượng của proton, neutron và khối lượng của hạt nhân \({}_{18}^{40}\text{Ar}\), \({}_{3}^{6}\text{Li}\) lần lượt là 1,0073 amu, 1,0087 amu và 39,9525 amu, 6,0145 amu. Lấy 1 amu = 931,5 MeV/c2. Năng lượng liên kết riêng của hạt nhân \({}_{18}^{40}\text{Ar}\) gấp x lần năng lượng liên kết riêng của hạt nhân \({}_{3}^{6}\text{Li}\). Giá trị của x là bao nhiêu (làm tròn kết quả đến chữ số hàng phần trăm)?
Cho phản ứng hạt nhân: \(_{11}^{23}Cl+_{1}^{2}D\to _{2}^{4}He+_{10}^{20}Ne\). Biết \({{m}_{Na}}=22,9327u\); \({{m}_{He}}=4,0015u\); \({{m}_{Ne}}=19,9870u\). ; \({{m}_{D}}=1,0073u\). Phản ứng trên tỏa hay thu một năng lượng bằng bao nhiêu?
Cho các hạt nhân sau \({}_{92}^{238}\text{U}\), \({}_{92}^{235}\text{U}\), \({}_{11}^{23}\text{Na}\), \({}_{79}^{197}\text{Au}\). Biết rằng khối lượng của các hạt nhân \({}_{92}^{238}\text{U}\), \({}_{92}^{235}\text{U}\), \({}_{11}^{23}\text{Na}\), \({}_{79}^{197}\text{Au}\) và khối lượng của proton, neutron lần lượt là \({{\text{m}}_{\text{U}238}}\) = 238,050788 amu; \({{\text{m}}_{\text{U}235}}\) = 234,993422 amu, \({{\text{m}}_{\text{Na}23}}\) = 22,983730 amu, \({{\text{m}}_{\text{Au}197}}\) = 196,966552 amu, mp = 1,007276 amu và mn = 1,008665 amu. Lấy \(1\text{ }\!\!~\!\!\text{ u}{{\text{c}}^{2}}=931,5\text{ }\!\!~\!\!\text{ MeV}\). Thứ tự sắp xếp các hạt nhân nói trên theo mức độ bền vững tăng dần là
Xét phản ứng tổng hợp hạt nhân: \(_{1}^{2}D+_{1}^{2}D\to _{2}^{3}He+_{0}^{1}n\). Biết rằng, khối lượng của các nguyên tử \(_{1}^{2}D\), \(_{2}^{4}He\) và khối lượng hạt neutron lần lượt là 2,0141u; 3,0160u; 1,0087u.
Biết rằng mỗi hạt nhân \(_{92}^{235}U\) phân hạch tỏa ra trung bình 200,0 MeV. Năng lượng tỏa ra khi tổng hợp hoàn toàn 1,00 g deterium theo phản ứng trên tương đương với năng lượng tỏa ra khi bao nhiêu gam \(_{92}^{235}U\) phân hạch hoàn toàn (làm tròn kết quả đến chữ số hàng phần trăm)?
Hạt nhân càng bền vững nếu nó có
Khối lượng của các hạt proton, neutron và hạt nhân \(_{8}^{18}O\) lần lượt là 1,0073 amu; 1,0087 amu; 17,9948 amu. Biết 1 amu = 931,5 MeV/c2.
Năng lượng liên kết của hạt nhân \(_{8}^{18}O\) là bao nhiêu MeV (làm tròn kết quả đến chữ số hàng đơn vị)?
Cho khối lượng hạt nhân \({}_{47}^{107}Ag\)là 106,8783 amu, của nơtrôn là 1,0087 amu; của prôtôn là 1,0073 amu. Độ hụt khối của hạt nhân \({}_{47}^{107}Ag\)là
Cho rằng khi một hạt nhân urani \({}_{92}^{235}U\) phân hạch thì toả ra năng lượng trung bình là 200 MeV, Lấy NA = 6,023.1023 mol-1, khối lượng mol của urani \({}_{92}^{235}U\)là 235 g/mol. Năng lượng tỏa ra khi phân hạch hết 1 kg urani \({}_{92}^{235}U\)là bao nhiêu? (\(\times \) 1026 MeV, làm tròn đến số thập phân thứ hai)
Với c là tốc độ ánh sáng trong chân không và m là khối lượng của một vật, hệ thức Einstein giữa năng lượng E và khối lượng m của vật là















