Số các các chỉnh hợp không lặp chập k của n là:

Gọi C là cô dâu, R là chú rể và 4 người bạn là A, B, D, E.

Tổng số cách xếp 6 người vào một hàng là 6! = 720 cách.

Trong một cách xếp bất kỳ, hoặc cô dâu đứng bên trái chú rể, hoặc chú rể đứng bên trái cô dâu. Số cách cô dâu đứng bên trái chú rể bằng số cách chú rể đứng bên trái cô dâu (tính chất đối xứng).

Vậy số cách xếp hàng mà cô dâu đứng bên trái chú rể là 720 / 2 = 360 cách.

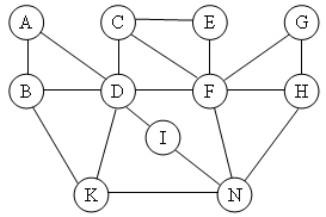
Thuật toán DFS (Depth-First Search - Tìm kiếm theo chiều sâu) bắt đầu từ một đỉnh và thăm các đỉnh kề của nó theo chiều sâu trước khi quay lui. Bắt đầu từ đỉnh A, ta có thể duyệt theo các hướng khác nhau, nhưng DFS sẽ đi sâu vào một nhánh trước khi xét các nhánh khác.

Bắt đầu từ A.

Chọn B (hoặc C, hoặc K, tùy cách duyệt). Giả sử chọn B.

Từ B, chọn D.

Từ D, chọn K.

Từ K, chọn I.

Từ I, chọn N.

Quay lui về K, không còn đỉnh nào để duyệt.

Quay lui về D, không còn đỉnh nào để duyệt.

Quay lui về B, chọn C.

Từ C, chọn E.

Từ E, chọn G.

Từ G, chọn H.

Từ E không còn đỉnh nào để duyệt.

Từ C chọn F.

Vậy, một thứ tự duyệt có thể là: A, B, D, K, I, N, C, E, G, H, F. Tuy nhiên, thứ tự này có thể khác nếu chọn các đỉnh kề khác nhau tại mỗi bước. Phương án 2 phù hợp nhất với cách duyệt DFS bắt đầu từ A, đi sâu vào một nhánh trước khi quay lại.

Các phương án khác không tuân theo đúng thứ tự duyệt của DFS.

Mô hình suy diễn

\(\frac{\begin{array}{l}
A \to B\\
A
\end{array}}{{\therefore B}}\)

tượng trưng cho quy tắc Modus Ponens, hay còn gọi là luật khẳng định. Trong đó, nếu ta có mệnh đề “A kéo theo B” (A → B) và A đúng, thì ta có thể suy ra B đúng.

• Luật rút gọn: Liên quan đến việc đơn giản hóa các mệnh đề phức tạp, thường là loại bỏ một phần của mệnh đề hội (A ∧ B).


• Luật cộng: Thêm một mệnh đề vào một mệnh đề đã có bằng phép tuyển (A → A ∨ B).


• Luật khẳng định: Chính là quy tắc Modus Ponens, như đã giải thích ở trên.


• Luật tam đoạn luận: Nếu A → B và B → C, thì A → C.

Do đó, đáp án đúng là luật khẳng định.