Đề thi thử Tốt nghiệp THPT năm 2025 môn Toán cụm trường miền Bắc - Đề 2
Câu 1
Gọi \(S\) là diện tích hình phẳng được tô đậm trong hình vẽ bên dưới.
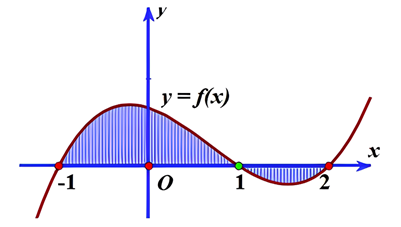
Công thức tính \(S\) là:
A.\(\int\limits_{-1}^{1}{f\left( x \right)dx}+\int\limits_{1}^{2}{f\left( x \right)dx}\).
B.\(\int\limits_{-1}^{1}{f\left( x \right)dx}-\int\limits_{1}^{2}{f\left( x \right)dx}\).
C.\(\int\limits_{-1}^{2}{f\left( x \right)dx}\).
D.\(-\int\limits_{-1}^{2}{f\left( x \right)dx}\).
Câu 2
Nếu\(\int\limits_{-1}^{5}{f\left( x \right)\text{d}x}=-3\) thì \(\int\limits_{5}^{-1}{f\left( x \right)\text{d}x}\) bằng:
A.\(5\).
B.\(4\).
C.\(-1\).
D.\(3\).
Câu 3
Trong không gian với hệ toạ độ \(Oxyz\), cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có đỉnh \(A\) trùng với gốc toạ độ \(O\), điểm \(B\left( 1;0;0 \right)\), \(D\left( 0;1;0 \right)\), \({D}'\left( 0;1;-1 \right)\). Toạ độ vectơ \(\overrightarrow{C{A}'}\) tương ứng là:
A.\(\left( -1;1;0 \right).\)
B.\(\left( 1;-1;-1 \right).\)
C.\(\left( -1;-1;-1 \right).\)
D.\(\left( 1;0;-1 \right).\)
Câu 4
Cho mặt phẳng \((P):2x+3y+5z-4=0\) và mặt phẳng \((Q)//(P)\). Vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng \((Q)\)?
A.\((2;3;-5)\).
B.\((2;-3;-5)\).
C.\((-4;-6;10)\).
D.\((4;6;10)\).
Câu 5
Giá trị nhỏ nhất của hàm số \(y=\frac{{{x}^{2}}+3}{x-1}\) trên đoạn \(\left[ 2;\,4 \right]\) là:
A.\(\underset{\left[ 2;\,4 \right]}{\mathop{\min }}\,y=6\).
B.\(\underset{\left[ 2;\,4 \right]}{\mathop{\min }}\,y=-2\).
C.\(\underset{\left[ 2;\,4 \right]}{\mathop{\min }}\,y=-3\).
D.\(\underset{\left[ 2;\,4 \right]}{\mathop{\min }}\,y=\frac{19}{3}\).
Câu 6
Điều tra \(42\) học sinh của một lớp \(11\) về số giờ tự học ở nhà, người ta có bảng sau đây:
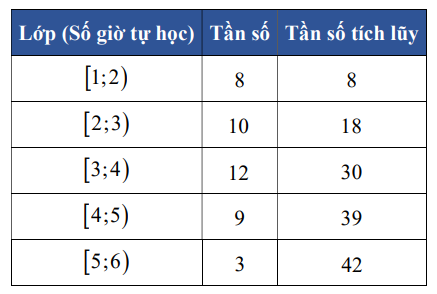
Số trung vị của mẫu số liệu là:
A.\(4,25\).
B.\(3,75\).
C.\(4,75\).
D.\(3,25\).
Câu 7
Trong không gian \(Oxyz\), phương trình đường thẳng đi qua hai điểm \(A\left( 1\,;2\,;3 \right),B\left( 5\,;4\,;-1 \right)\) là:
A.\(\frac{x-1}{4}=\frac{y-2}{2}=\frac{z-3}{4}.\)
B.\(\frac{x-5}{2}=\frac{y-4}{1}=\frac{z+1}{-2}.\)
C.\(\frac{x+5}{-2}=\frac{y+4}{-1}=\frac{z-1}{2}.\)
D.\(\frac{x+1}{4}=\frac{y+2}{2}=\frac{z+3}{-4}.\)
Câu 8
Số nghiệm nguyên dương của bất phương trình \({{\log }_{\frac{1}{3}}}\left( x-3 \right)\ge {{\log }_{\frac{1}{3}}}4\)
A.\(5\).
B.\(7\).
C.\(3\).
D.\(4\).
Câu 9
Hàm số nào dưới đây có đồ thị như trong hình vẽ bên?
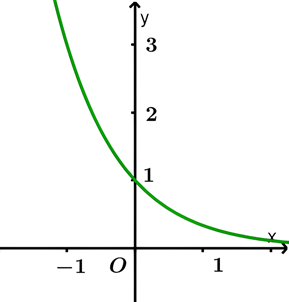 A.
A.\(y={{3}^{x}}\).
B.\(y={{\left( \frac{1}{3} \right)}^{x}}\).
C.\(y={{\log }_{\frac{1}{3}}}x\).
D.\(y={{\log }_{3}}x\).
Câu 10
Cho cấp số nhân \(\left( {{u}_{n}} \right)\) biết \({{u}_{1}}=2\) và công bội \(q=3\). Dãy số nào sau đây là cấp số nhân đó?
A.\(2;6;9;12;15\)…
B.\(2;6;18;24;32\)…
C.\(2;6;18;54;162\)…
D.\(2;6;16;54;108\)…
Câu 11
Trong không gian với hệ trục tọa độ \(Oxyz\), mặt cầu tâm \(I\left( 3;\,-1;\,0 \right)\), bán kính \(R=5\) có phương trình là:
A.\({{\left( x+3 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{z}^{2}}=5\).
B.\({{\left( x-3 \right)}^{2}}+{{\left( y+1 \right)}^{2}}+{{z}^{2}}=5\).
C.\({{\left( x-3 \right)}^{2}}+{{\left( y+1 \right)}^{2}}+{{z}^{2}}=25\).
D.\({{\left( x+3 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{z}^{2}}=25\).
Câu 12
Đồ thị hàm số \(y=\frac{{{x}^{2}}+2x+2}{x+1}\) có tiệm cận xiên là đường thẳng:
A.\(y=x\).
B.\(y=x-1\).
C.\(y=2x-1\)
D.\(y=x+1\).
Câu 13
Cho hàm số \(f\left( x \right)=\frac{-2x+3}{x-2}\).
a) Hàm số đồng biến trên \(\mathbb{R}\backslash \left\{ 2 \right\}\).
b) Đồ thị hàm số cắt trục tung tại điểm \(M\left( 0;\frac{-3}{2} \right)\).
c) Đồ thị hàm số \(y=f\left( x \right)\) cắt đường thẳng \(y=x\) tại hai điểm phân biệt khi.
d) Đồ thị hàm số \(y=f\left( x \right)\) cắt đường thẳng \(y=x+2\) tại hai điểm phân biệt M và N. Biết I là trung điểm của đoạn thẳng \(MN\). Khi đó hoành độ của điểm I là \(-1\).
Câu 14
Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( 2;1;3 \right)\),\(B\left( 3;0;2 \right)\), \(C\left( 0;-2;1 \right)\).
a) Tọa độ các vectơ \(\overrightarrow{AB}=\left( 1;-1;-1 \right),\overrightarrow{AC}=\left( -2;-3;-2 \right)\).
b) Phương trình mặt phẳng \(\left( ABC \right)\) là \(x-4y+5z-13=0\).
c) Khoảng cách từ điểm \(A\) đến mặt phẳng trung trực của đoạn thẳng \(BC\) bằng \(\frac{\sqrt{17}}{4}\).
d) Mặt phẳng \(\left( P \right)\) đi qua \(A,\,B\) và cách \(C\) một khoảng lớn nhất có phương trình \(3x+2y+z-11=0\).
Câu 15
Từ một hộp có \(4\) quả cầu đỏ và \(6\) quả cầu xanh. Ông X bốc ngẫu nhiên ra hai quả cầu thì thấy có quả cầu đỏ. Xét 2 biến cố:
A: "Ông X bốc được quả cầu xanh",
B: "Ông X bốc được quả cầu đỏ".
a) Số phần tử của không gian mẫu: \(n\left( \Omega \right)=C_{4}^{1}.C_{6}^{1}=36\).
b) \(n(B)=C_{4}^{1}.C_{6}^{1}+C_{4}^{2}\).
c) \(n(A\cap B)=C_{4}^{1}.C_{6}^{1}\).
d) Xác suất ông \(X\) bốc được quả cầu xanh là: \(P\left( A|B \right)=\frac{C_{4}^{1}.C_{6}^{1}}{C_{4}^{1}.C_{6}^{1}+C_{4}^{2}}\).
Câu 16
Một vật chuyển động trong \(3\) giờ với vận tốc \(v\) (km/h) phụ thuộc thời gian \(t\) (h). Trong khoảng thời gian \(1\) giờ kể từ khi bắt đầu chuyển động, vận tốc của nó là \(v=-\frac{5}{4}{{t}^{2}}+5t+4\); trong khoảng thời gian còn lại vật chuyển động đều.
a) Gia tốc của vật trong khoảng thời gian \(1\) giờ kể từ khi bắt đầu chuyển động bằng \(0\).
b) Gia tốc của vật trong khoảng thời gian từ \(1\) giờ đến \(3\) giờ bằng \(0\).
c) Vận tốc của vật trong khoảng thời gian từ \(1\) giờ đến \(3\) giờ bằng \(7,75\)(km/h).
d) Quãng đường mà vật chuyển động trong khoảng thời gian \(1\) giờ kể từ khi bắt đầu chuyển động lớn hơn \(4\)(km).
Top 10/0 lượt thi
| Tên | Điểm | Thời gian |
|---|