Câu hỏi:

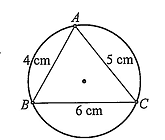
Từ một miếng bìa hình tròn, bạn Nam cắt ra một hình tam giác $ABC$ có độ dài các cạnh $AB=4$ cm, $AC=5$ cm, $BC=6$ cm. Tính bán kính $R$ của miếng bìa ban đầu (Làm tròn kết quả đến hàng đơn vị của cm)

Trả lời:

Đáp án đúng:

Áp dụng định lí côsin cho tam giác $A B C$, ta có:

$\cos A=\frac{A B^2+A C^2-B C^2}{2 A B \cdot A C}=\frac{4^2+5^2-6^2}{2 \cdot 4 \cdot 5}=\frac{1}{8}$
Mà $\widehat{A}<180^{\circ}$ nên $\sin A=\sqrt{1-\cos ^2 A}=\sqrt{1-\frac{1}{64}}=\frac{3 \sqrt{7}}{8}$.
Áp dụng định lí sin, ta có:

$\frac{B C}{\sin A}=2 R \Rightarrow R=\frac{B C}{2 \sin A}=\frac{6}{2 \cdot \frac{3 \sqrt{7}}{8}} \approx 3(\mathrm{~cm})$

Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài

20+ Câu trắc nghiệm giữa HK1 Toán 10 - CTST - Đề 2

18/09/2025

0 lượt thi

0 / 22

Bắt đầu thi

Câu hỏi liên quan

Câu 1:

Các giá trị của $x$ để mệnh đề chứa biến $P\left(x \right)$ : " $x$ là số tự nhiên thỏa mãn $x^4-5x^2+4=0$ " đúng là

Lời giải:

Đáp án đúng: C

Ta có phương trình $x^4 - 5x^2 + 4 = 0$. Đặt $t = x^2$, $t \ge 0$. Khi đó phương trình trở thành $t^2 - 5t + 4 = 0$.

Phương trình này có hai nghiệm $t_1 = 1$ và $t_2 = 4$.

Với $t_1 = 1$, ta có $x^2 = 1$ suy ra $x = \pm 1$.

Với $t_2 = 4$, ta có $x^2 = 4$ suy ra $x = \pm 2$.

Vậy tập nghiệm của phương trình là $x \in \{-2, -1, 1, 2\}$.

Vì $x$ là số tự nhiên nên $x \in \{1, 2\}$.

Câu 2:

Số phần tử của tập hợp $A=\Big\{ k^2+1 \, \big| \, k \in \mathbb{Z}, \, |k| \le 2 \Big\}$ là

Lời giải:

Đáp án đúng: D

Ta có $|k| \le 2$ nên $k \in \{-2, -1, 0, 1, 2\}$.

Khi đó:

$k = -2 \Rightarrow k^2 + 1 = (-2)^2 + 1 = 5$

$k = -1 \Rightarrow k^2 + 1 = (-1)^2 + 1 = 2$

$k = 0 \Rightarrow k^2 + 1 = 0^2 + 1 = 1$

$k = 1 \Rightarrow k^2 + 1 = 1^2 + 1 = 2$

$k = 2 \Rightarrow k^2 + 1 = 2^2 + 1 = 5$

Vậy $A = \{1, 2, 5\}$. Số phần tử của tập $A$ là 3.

Câu 3:

Cho tập hợp $X=\left\{ a;b \right\}, \, Y=\left\{ a;b;c \right\}$ . $X \cup Y$ là tập hợp nào sau đây?

Lời giải:

Đáp án đúng: C

Phép hợp của hai tập hợp $X$ và $Y$, ký hiệu $X \cup Y$, là tập hợp chứa tất cả các phần tử thuộc $X$ hoặc thuộc $Y$ (hoặc thuộc cả hai).

Trong trường hợp này:

$X = \{a; b\}$

$Y = \{a; b; c\}$

Do đó, $X \cup Y = \{a; b; c\}$.

Câu 4:

Tập hợp $P=\Big\{ x \in \mathbb{R} \, \big| \, -1< 2x+1 \le 11\Big\}$ được viết lại dưới dạng đoạn, khoảng, nửa khoảng là

Lời giải:

Đáp án đúng: C

Ta có:

$-1 < 2x + 1 \le 11$

$-1 - 1 < 2x \le 11 - 1$

$-2 < 2x \le 10$

$-1 < x \le 5$

Vậy tập hợp $P$ được viết lại là $(-1; 5]$.

Câu 5:

Tọa độ đỉnh của parabol $y=-3x^2+2x+1$ là

Lời giải:

Đáp án đúng: C

Để tìm tọa độ đỉnh của parabol $y = ax^2 + bx + c$, ta sử dụng công thức:

Hoành độ đỉnh: $x_I = -\dfrac{b}{2a}$

Tung độ đỉnh: $y_I = -\dfrac{\Delta}{4a}$ hoặc $y_I = f(x_I)$

Trong trường hợp này, ta có $a = -3$, $b = 2$, và $c = 1$.

Tính hoành độ đỉnh:
$x_I = -\dfrac{2}{2(-3)} = \dfrac{1}{3}$

Tính tung độ đỉnh:
$y_I = -3\left(\dfrac{1}{3}\right)^2 + 2\left(\dfrac{1}{3}\right) + 1 = -3\left(\dfrac{1}{9}\right) + \dfrac{2}{3} + 1 = -\dfrac{1}{3} + \dfrac{2}{3} + 1 = \dfrac{1}{3} + 1 = \dfrac{4}{3}$

Vậy, tọa độ đỉnh của parabol là $I\left(\dfrac{1}{3}; \dfrac{4}{3}\right)$.

Câu 6:

Cho tam giác $ABC$ có $AB=5, \, BC=7, \, AC=8$ . Số đo của góc $A$ là

Lời giải: