Câu hỏi:
Cho tập hợp \(A = \left\{ {0;2} \right\}\). Khẳng định nào sau đây sai?
Đáp án đúng: D
Vì 2 là phần tử nên kí hiệu đúng là \(2 \in A\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Học Kì I - Toán 10 - Chân Trời Sáng Tạo - Bộ Đề 01 là bài kiểm tra trắc nghiệm online được thiết kế theo cấu trúc mới của Bộ Giáo dục và Đào tạo. Đề thi bao gồm nhiều dạng câu hỏi như: nhiều phương án lựa chọn, đúng sai, trả lời ngắn và tự luận. Mỗi câu hỏi tập trung vào các kiến thức trọng tâm của chương trình Toán lớp 10, giúp học sinh ôn tập và củng cố kiến thức một cách hiệu quả. Đề thi không chỉ kiểm tra khả năng lý thuyết mà còn đánh giá khả năng giải quyết vấn đề thực tế của học sinh.
Câu hỏi liên quan
Trong một cuộc thi thể thao, người ta ghi lại thời gian hoàn thành chặng đường đua của một số vận động viên ở bảng sau:
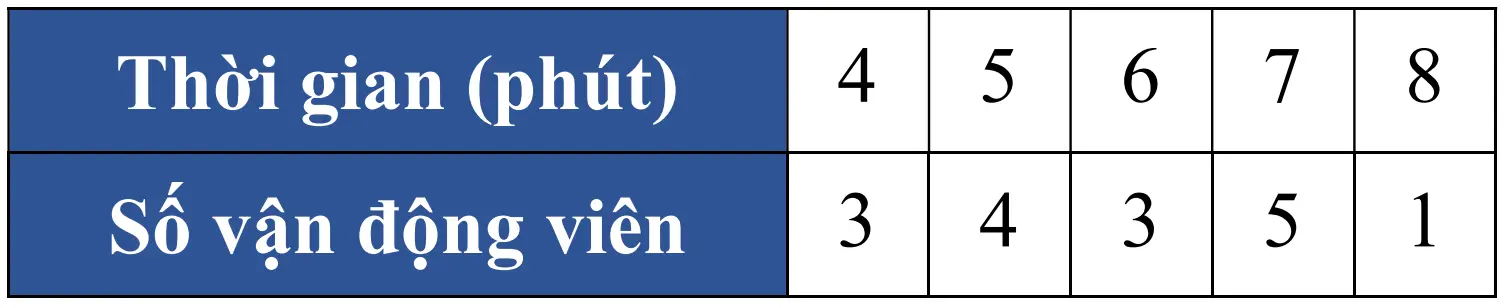
Xét tính đúng/sai của các mệnh đề sau:
Mốt của mẫu số liệu trên là 7
Độ lệch chuẩn (làm tròn đến hàng phần trăm) của mẫu số liệu trên là \(1,23\)
Tứ phân vị thứ nhất và thứ ba của mẫu số liệu trên lần lượt là 5 và 6
Khoảng tứ phân vị của mẫu số liệu trên là 2
a) Đúng.
Vì giá trị 7 có tần số lớn nhất (bằng 5) nên \({M_0} = 7\).
b) Sai.
Tổng số vận động viên là \(n = 3 + 4 + 3 + 5 + 1 = 16\).
Số trung bình của mẫu số liệu là:
\(\bar x = \frac{{3.4 + 4.5 + 3.6 + 5.7 + 8}}{{16}} = 5,8125\).
Phương sai của mẫu số liệu là:
\({s^2} = \frac{{\left[ \begin{array}{l}3{(4 - 5,8125)^2} + 4{(5 - 5,8125)^2} + 3{(6 - 5,8125)^2}\\ + 5{(7 - 5,8125)^2} + {(8 - 5,8125)^2}\end{array} \right]}}{{16}} = \frac{{391}}{{256}}\).
Độ lệch chuẩn của mẫu số liệu là:
\(s = \sqrt {\frac{{391}}{{256}}} \approx 1,24\).
c) Sai + d) Đúng.
Gọi \({x_1},\,{x_2},\, \ldots ,\,{x_{16}}\) là thời gian của các vận động viên được sắp xếp theo thứ tự không giảm.
Vì cỡ mẫu \(n = 16\) là số chẵn nên trung vị của mẫu số liệu là trung bình cộng của giá trị \({x_8}\) và \({x_9}\) như trong bảng số liệu.
Ta thấy hai giá trị này đều bằng 6.
Suy ra \({M_e} = \frac{{6 + 6}}{2} = 6\).
• Xét dãy số liệu từ \({x_1}\) đến \({x_8}\).
Tứ phân vị thứ nhất là trung vị của dãy số liệu này và \({Q_1} = \frac{{{x_4} + {x_5}}}{2} = 5\).
• Xét dãy số liệu từ \({x_9}\) đến \({x_{16}}\).
Tứ phân vị thứ ba là trung vị của dãy số liệu này và \({Q_3} = \frac{{{x_{12}} + {x_{13}}}}{2} = 7\).
Vậy khoảng tứ phân vị là: \({{\rm{\Delta }}_Q} = {Q_3} - {Q_1} = 7 - 5 = 2\).
Chùa Ông Núi - ngôi cổ tự linh thiêng danh tiếng ở Bình Định, tọa lạc tại đỉnh Chóp Vung, huyện Phù Cát, tỉnh Bình Định và cách thành phố Quy Nhơn 30 km. Điểm nổi bật nhất của chùa chính là bức tượng Phật ngồi lớn nhất Đông Nam Á.
Để tính chiều cao AB của bức tượng, người ta đo ở hai vị trí C và D cách nhau 200 m. Tại C người ta đo được \(BCE = {52^ \circ },\,ACE = {67^ \circ }\) tại D người ta đo được \(BDC = {23^ \circ }\) (như hình vẽ).

Xét tính đúng/sai của các mệnh đề sau:
\(\widehat {CBD} = {29^ \circ }\)
Độ dài cạnh BC (làm tròn đến hàng đơn vị) là 162 m
\(\widehat {BAC} = {24^ \circ }\)
Chiều cao của bức tượng (làm tròn đến hàng đơn vị) là 107 m
Mô hình hóa bài toán bởi hình vẽ sau.

a) Đúng.
Ta có \(\widehat {BCD} = {180^ \circ } - \widehat {BCE} = {180^ \circ } - {52^ \circ } = {128^ \circ }\).
Suy ra \(\widehat {CBD} = {180^ \circ } - \widehat {BCD} - \widehat {BDC} = {29^ \circ }\).
b) Sai.
Áp dụng định lí sin cho tam giác BCD ta có:
\(\frac{{BC}}{{{\rm{sin}}\widehat {BDC}}} = \frac{{CD}}{{{\rm{sin}}\widehat {CBD}}}\)
\( \Rightarrow BC = \frac{{CD}}{{{\rm{sin}}\widehat {CBD}}}.{\rm{sin}}\widehat {BDC} = \frac{{200}}{{{\rm{sin}}{{29}^ \circ }}}.{\rm{sin}}{23^ \circ } \approx 161\) (m).
c) Sai.
Tam giác BCE vuông tại E, có \(\widehat {EBC} = {90^ \circ } - \widehat {BCE} = {38^ \circ }\).
Suy ra \(\widehat {ABC} = {180^ \circ } - \widehat {EBC} = {142^ \circ }\).
Ta có \(\widehat {ACB} = \widehat {ACE} - \widehat {BCE} = {67^ \circ } - {52^ \circ } = {15^ \circ }\).
Tam giác ABC có \(\widehat {BAC} = {180^ \circ } - \widehat {ACB} - \widehat {ABC} = {23^ \circ }\).
d) Đúng.
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{{BC}}{{{\rm{sin}}\widehat {BAC}}} = \frac{{AB}}{{{\rm{sin}}\widehat {ACB}}}\)
\( \Rightarrow AB = \frac{{BC}}{{{\rm{sin}}\widehat {BAC}}}.{\rm{sin}}\widehat {ACB} \approx 107\) m.
Vậy chiều cao của bức tượng gần bằng 107 m.
Sắp xếp mẫu số liệu theo thứ tự không giảm ta có:
16; 22; 29; 30; 31; 31; 32; 32; 32; 36; 41; 47.
Cỡ mẫu \(n = 12\).
• Trung vị của mẫu số liệu là: \({M_e} = {Q_2} = \frac{{31 + 32}}{2} = 31,5\).
• Xét dãy số liệu: 16; 22; 29; 30; 31; 31.
Tứ phân vị thứ nhất là trung vị của dãy số liệu trên, do đó:
\({Q_1} = \frac{{29 + 30}}{2} = 29,5\).
• Xét dãy số liệu: 32; 32; 32; 36; 41; 47.
Tứ phân vị thứ ba là trung vị của dãy số liệu trên, do đó:
\({Q_3} = \frac{{32 + 36}}{2} = 34\).
• Khoảng tứ phân vị là: \({{\rm{\Delta }}_Q} = {Q_3} - {Q_1} = 34 - 29,5 = 4,5\).
• Xác định giá trị ngoại lệ.
Ta có cận dưới: \({Q_1} - 1,5{{\rm{\Delta }}_Q} = 29,5 - 1,5.4,5 = 29,5 - 6,75 = 22,75\).
Cận trên: \({Q_3} + 1,5.{{\rm{\Delta }}_Q} = 34 + 6,75 = 40,75\).
Ta thấy giá trị nhỏ hơn \(22,75\) hoặc lớn hơn \(40,75\) là ngoại lệ.
Các giá trị nhỏ hơn \(22,75\) gồm 16 và 22.
Các giá trị lớn hơn \(40,75\) gồm 41 và 47.
Vậy có 4 giá trị ngoại lệ là 16; 22; 41; 47.
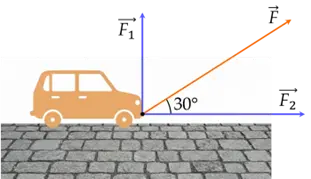
\({\rm{cos}}{30^ \circ } = \frac{{\sqrt 3 }}{2}\).
\( \Rightarrow {F_2} = 50{\rm{cos}}{30^ \circ } = 50.\frac{{\sqrt 3 }}{2} = 25\sqrt 3 \).
Công sinh bởi \(\overrightarrow {{F_2}} \) khi vật chuyển động một quãng đường \(s = 250\) m là:
\(A = {F_2}.s = 25\sqrt 3 .250 = \left( {25.250} \right)\sqrt 3 = 6\,250\sqrt 3 \).
Từ đây ta có \(a = 6\,250,\,b = 3\).
Vậy \(a + b = 6\,250 + 3 = 6\,253\).
Gọi x là số lần tăng giá \(\left( {x \ge 0} \right)\). Khi đó:
+ Giá bán mỗi chiếc là \(34\,000 + 1\,000x\) (đồng).
+ Số lượng bán mỗi tháng là \(3\,000 - 100x\) (chiếc).
+ Lợi nhuận trên mỗi chiếc là
\(34\,000 + 1\,000x - 20\,000 = 14\,000 + 1\,000x\) (đồng).
Tổng lợi nhuận thu được là:
\(14\,000 + 1\,000x)\left( {3\,000 - 100x} \right) \Leftrightarrow 42\,000\,000 + 1\,600\,000x - 100\,000{x^2}\).
Xét hàm số \(f\left( x \right) = 42\,000\,000 + 1\,600\,000x - 100\,000{x^2}\).
Hàm số f(x) là một parabol có hệ số \(a = - 100\,000 < 0\) nên có bề lõm quay xuống.
Khi đó f(x) đạt giá trị lớn nhất tại \(x = \frac{{1\,600\,000}}{{2.100\,000}} = 8\).
Suy ra,
\({\rm{max}}f\left( x \right) = f\left( 8 \right) = 42\,000\,000 + 1\,600\,000.8 - 100\,{000.8^2} = 48\,400\,000\) (đồng).
Vậy lợi nhuận lớn nhất bằng \(48\,400\,000\) đồng hay \(48,4\) triệu đồng.
Cho đồ thị hàm số \(y = 2{x^2} + 6x + 5\). Xét tính đúng/sai của các mệnh đề sau:
Đỉnh là \(I\left( { - \frac{3}{2};\frac{1}{2}} \right)\)
Đồ thị của hàm số là:
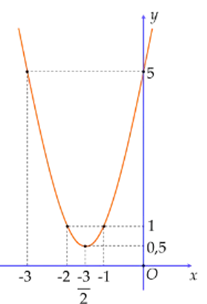
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - \frac{3}{2}} \right)\)
Hàm số đồng biến trên khoảng \(\left( { - \frac{3}{2}; + \infty } \right)\)

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Địa Lí 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026
ĐĂNG KÝ GÓI THI VIP
- Truy cập hơn 100K đề thi thử và chính thức các năm
- 2M câu hỏi theo các mức độ: Nhận biết – Thông hiểu – Vận dụng
- Học nhanh với 10K Flashcard Tiếng Anh theo bộ sách và chủ đề
- Đầy đủ: Mầm non – Phổ thông (K12) – Đại học – Người đi làm
- Tải toàn bộ tài liệu trên TaiLieu.VN
- Loại bỏ quảng cáo để tăng khả năng tập trung ôn luyện
- Tặng 15 ngày khi đăng ký gói 3 tháng, 30 ngày với gói 6 tháng và 60 ngày với gói 12 tháng.