Biết \({}_{6}^{14}C\) là đồng vị phóng xạ \({{\beta }^{-}}\) với chu kì bán rã là 5 730 năm (lấy 1 năm có 365 ngày). Một mẫu than nặng 5 g lấy từ một hố lửa cổ có độ phóng xạ ₁₄C là 53,0 (phân rã/phút). Một cái cây còn sống có độ phóng xạ ₁₄C là 15,3 (phân rã/phút) cho mỗi gram (g).

Tuổi của mẫu than lấy từ hố lửa cổ nói trên là bao nhiêu năm (làm tròn kết quả đến hàng trăm)?

 

Máy xạ trị (như hình bên) thường sử dụng nguồn phóng xạ \({ }_{27}^{60} \mathrm{Co}\) có chu kì bán rã là 5,3 năm. Để đáp ứng đúng các tiêu chí y học để điều trị bệnh, thiết bị sẽ bắt buộc phải bảo dưỡng để hiệu chỉnh lại chùm tia chiếu xạ trước khi độ phóng xạ giảm đi \(7 \%\) và phải thay nguồn phóng xạ mới trước khi độ phóng xạ giảm đi \(50 \%\). Lấy 1 năm = 12 tháng. Biết mỗi lần bảo dưỡng không làm ảnh hưởng đến nguồn phóng xạ.

Khoảng thời gian tối đa phải thực hiện bảo dưỡng máy xạ trị lần tiếp theo (gọi là chu kì bảo dưỡng) theo đơn vị tháng (lấy phần nguyên) bẳng bao nhiêu ?

Trong không khí, tia phóng xạ nào sau đây có tốc độ nhỏ nhất?

Nguồn phóng xạ \(\alpha\) americium \({ }_{95}^{241} \mathrm{Am}\) có hằng số phóng xạ \(5,081 \cdot 10^{-11}(1 / \mathrm{s})\) được đặt giữa hai bản kim loại kết nối với một pin. Các hạt \(\alpha\) phóng ra làm ion hóa không khí giữa hai bản kim loại, cho phép một dòng điện nhỏ chạy giữa hai bản kim loại đó và chuông báo không kêu.

Nếu có khói bay vào giữa hai bản kim loại, các ion trong này sẽ kết hợp với những phân tử khói và dịch chuyển chậm hơn làm cường độ dòng điện chạy giữa hai bản kim loại giảm đi. Khi dòng điện giảm tới mức nhất định thì cảm biến báo khói sẽ gửi tín hiệu kích hoạt chuông báo cháy.

Khảo sát một mẫu đá uraninite với thành phần ban đầu chỉ gồm \({}_{92}^{238}\text{U}\). Tỉ lệ khối lượng \({}_{92}^{238}\text{U}\) còn lại và khối lượng \({}_{82}^{206}\text{Pb}\) là \(0,0453\). Chu kỳ bán rã của \({}_{92}^{238}\text{U}\) là \(4,{{5592.10}^{9}}~\text{n }\!\!\breve{\mathrm{a}}\!\!\text{ m}\). Khối lượng mol của \({}_{92}^{238}\text{U}\) là \(238\text{ }\!\!~\!\!\text{ g}/\text{mol}\), khối lượng mol của \({}_{82}^{206}\text{Pb}\) là \(206\text{ }\!\!~\!\!\text{ g}/\text{mol}\).

Tuổi của mẫu đá uraninite trên là \(z{{.10}^{10}}\text{ }\!\!~\!\!\text{ n }\!\!\breve{\mathrm{a}}\!\!\text{ m}\). Giá trị của \(z\) là bao nhiêu (làm tròn kết quả đến chữ số hàng phần trăm)?

Công thức \(H=\lambda N\) thể hiện mối quan hệ giữa các đại lượng là

Các nhà khoa học đã xác định được độ phóng xạ của 1 g mẫu Carbon trong cơ thể sinh vật sống là \(0,231 \mathrm{~Bq}\). Biết rằng, trong số các đồng vị của Carbon có trong mẫu, chỉ có \({ }_{6}^{14} \mathrm{C}\) là đồng vị phóng xạ với chu kì bán rã là 5730 năm (lấy 1 năm có 365 ngày).

Số nguyên tử \({ }_{6}^{14} \mathrm{C}\) có trong 1 g mẫu Carbon trong cơ thể sinh vật sống bằng \(\mathrm{x} \cdot 10^{10}\) nguyên tử. Tìm x (làm tròn đến hàng phần trăm).

Vào ngày 19/9/1991, trong khi đang tìm đường vượt qua dãy Otzal Alps, hai nhà leo núi người Đức đã phát hiện thấy xác ướp người cổ được bảo quản hầu như nguyên vẹn trong băng tuyết tại Hauslabjoch, khu vực giữa biên giới Áo và Italia. Xác ướp đó được đặt tên là người băng Otzi.

Tại thời điểm này, các nhà khoa học đã đo được độ phóng xạ của 1 g mẫu Carbon trong cơ thể người băng Otzi là \(0,121 \mathrm{~Bq}\). Xác định niên đại của người băng đó theo đơn vị năm (làm tròn đến hàng trăm).

Trong các biển báo dưới đây, đâu là biển báo nguy hiểm do phóng xạ?

Tại một bệnh viện tuyến tỉnh, một bệnh nhân nữ 45 tuổi được chỉ định chụp PET để kiểm tra nghi ngờ di căn tuyến giáp. Do có sự chậm trễ trong quá trình vận chuyển và chuẩn bị, bệnh nhân được tiêm 1 ml dung dịch chứa đồng vị phóng xạ \({}_{\text{ }\!\!~\!\!\text{ }}^{18}\text{F}\) sau 3 giờ kể từ khi pha chế. Biết hoạt độ của mẫu tại thời điểm vừa pha chế là 150 MBq và chu kỳ bán rã của \({}_{\text{ }\!\!~\!\!\text{ }}^{18}\text{F}\) là 110 phút.

Độ phóng xạ của mẫu tại thời điểm tiêm bằng bao nhiêu MBq? (Làm tròn đến chữ số hàng đơn vị)

Một mẫu chất phóng xạ có chu kỳ bán rã 5 giờ. Ban đầu, số lượng hạt nhân của chất này là N₀ = 10²⁰ hạt nhân. Số hạt nhân còn lại sau 10 giờ là

Tia phóng xạ nào có bản chất là sóng điện từ?

Năm 1947, Willand Frank Libby đã tìm ra phương pháp xác định niên đại của các cổ vật gốc hữu cơ dựa vào các đặc tính của đồng vị phóng xạ \({ }_{6}^{14} \mathrm{C}\). Sau khi kiểm tra một mẫu xương cổ chứa \({ }_{6}^{14} \mathrm{C}\) với hoạt độ ban đầu là 1500 Bq , người ta biết được hoạt độ \({ }_{6}^{14} \mathrm{C}\) còn lại trong mẫu xương cổ là 500 Bq . Biết đồng vị \({ }_{6}^{14} \mathrm{C}\) có chu kỳ bán rã là 5730 năm. Tuổi thọ của mẫu xương cổ trên là bao nhiêu năm? (kết quả làm tròn đến chữ số hàng đơn vị).

Một phòng thí nghiệm, ban đầu mua về một mẫu polonium có chứa 2,1 g \({}_{84}^{210}\text{Po}\). Các hạt nhân \({}_{84}^{210}\text{Po}\) phóng xạ \(\text{ }\!\!\alpha\!\!\text{ }\) và biến thành hạt nhân X. Biết rằng trong 1 năm sau đó nó tạo ra 0,0084 mol khí He. Chu kì bán rã của \({}_{84}^{210}\text{Po}\) là bao nhiêu ngày (lấy 1 năm = 365 ngày, làm tròn kết quả đến chữ số hàng đơn vị)?

Tia gamma là bức xạ điện từ có bước sóng rất ngắn với khả năng đâm xuyên lớn qua các vật liệu. Người ta ứng dụng khả năng đâm xuyên của chùm tia gamma để ứng dụng trong các phép đo bề dày của vật liệu. Một chùm tia gamma với cường độ ban đầu I0 sau khi đi qua một lớp vật liệu có chiều dày x(m) thì cường độ chùm tia gamma giảm tới giá trị I. Cường độ chùm tia gamma bị suy giảm sau khi đi qua lớp vật liệu được cho bởi công thức

 \(I={{I}_{0}}.{{e}^{-\mu .x}}\)

Trong đó \(\mu \) (m^-1) là hệ số hấp thụ bức xạ của môi trường. Giả sử sau khi đi qua lớp vật liệu thì cường độ chùm tia gamma giảm 20%. Hãy xác định bề dày của lớp vật liệu. Cho biết hệ số hấp thụ bức xạ của vật liệu là 0,4.

Polonium \(_{84}^{210}Po\) là một chất phóng xạ \(\alpha \) có chu kì bán rã 138 ngày và biến đổi thành hạt nhân chì \(_{82}^{206}Pb\). Ban đầu \(\left( t=0 \right)\), một mẫu có khối lượng 85 g, trong đó 40% khối lượng của mẫu là chất phóng xạ \(_{84}^{210}Po\), phần còn lại không có tính phóng xạ. Giả sử toàn bộ các hạt \(\alpha \) sinh ra trong quá trình phóng xạ đều thoát ra khỏi mẫu.

Khối lượng của mẫu tại thời điểm \(t=276\) ngày là bao nhiêu gam (làm tròn kết quả đến chữ số hàng phần mười)?

Đồ thị trong hình bên biểu diễn sự thay đổi độ phóng xạ của một mẫu chất phóng xạ b+ theo thời gian. Ban đầu (tại thời điểm \(\text{t}=0\) s) mẫu chất phóng xạ này nguyên chất.

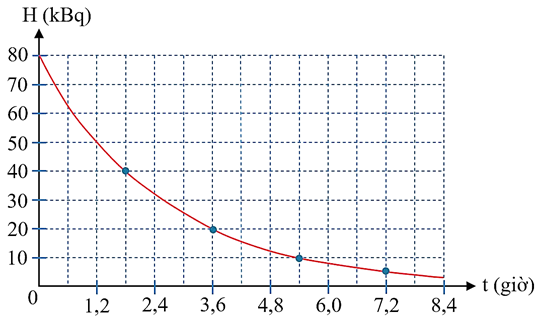
Technitium \({}_{\text{43}}^{\text{99}}\text{Tc}\)là đồng vị phóng xạ đánh dấu được sử dụng trong chẩn đoán và điều trị các bệnh liên quan đến tuyến giáp, cơ tim, phổi, gan... Một bệnh nhân được tiêm liều dược chất chứa technitium \({}_{\text{43}}^{\text{99}}\text{Tc}\)với độ phóng xạ 400 MBq. Cho chu kì bán rã của technitium \({}_{\text{43}}^{\text{99}}\text{Tc}\)là 6,01 giờ. Khối lượng chất technitium \({}_{\text{43}}^{\text{99}}\text{Tc}\)có trong liều dược chất phóng xạ đó là bao nhiêu nanogram (kết quả làm tròn đến hàng phần trăm)?

Poloni \({}_{84}^{210}\text{Po}\) là một chất phóng xạ α có chu kì bán rã 138 ngày và biến đổi thành hạt nhân chì \({}_{82}^{206}\text{Pb}\). Ban đầu \(\left( t~=~0 \right)\), một mẫu có khối lượng 85,0 g, trong đó 40% khối lượng của mẫu là chất phóng xạ \({}_{84}^{210}\text{Po}\), phần còn lại không có tính phóng xạ. Giả sử toàn bộ các hạt α sinh ra trong quá trình phóng xạ đều thoát ra khỏi mẫu.

Độ phóng xạ của mẫu tại thời điểm ban đầu là \(x{{.10}^{14}}\text{Bq}\). Tìm \(x\) (kết quả làm tròn đến hàng đơn vị).  

Tại một bệnh viện tuyến tỉnh, một bệnh nhân nữ 45 tuổi được chỉ định chụp PET để kiểm tra nghi ngờ di căn tuyến giáp. Do có sự chậm trễ trong quá trình vận chuyển và chuẩn bị, bệnh nhân được tiêm 1 ml dung dịch chứa đồng vị phóng xạ \({}_{\text{ }\!\!~\!\!\text{ }}^{18}\text{F}\) sau 3 giờ kể từ khi pha chế. Biết hoạt độ của mẫu tại thời điểm vừa pha chế là 150 MBq và chu kỳ bán rã của \({}_{\text{ }\!\!~\!\!\text{ }}^{18}\text{F}\) là 110 phút.

Để đảm bảo an toàn cho bệnh nhân, Bộ Y tế quy định giới hạn liều hiệu dụng tối đa là 1,8 mSv cho mỗi lần chụp PET. Biết rằng mỗi MBq của \({}_{\text{ }\!\!~\!\!\text{ }}^{18}\text{F}\) gây ra 0,019 mSv liều hiệu dụng. Thời gian tối thiểu kể từ lúc pha chế mà liều ban đầu có thể được tiêm toàn bộ cho bệnh nhân là bao nhiêu phút? (Làm tròn đến hàng đơn vị)

Có 3 loại tia phóng xạ, bao gồm: tia alpha, tia beta và tia gamma.

Tia phóng xạ nào không bị lệch hướng khi đi qua điện trường?

Đồng vị xenon (\(^{133}\)Xe) là chất phóng xạ \(\beta^-\) có chu kì bán rã là 5,24 ngày. Trong y học, hỗn hợp khí chứa xenon được sử dụng để dánh giá độ thông khí của phổi người bệnh. Một người bệnh được chỉ định sử dụng liều xenon có độ phóng xạ 3,18.10\(^8\) Bq. Coi rằng 85,0% lượng xenon trong liều đó lắng đọng tại phổi. Người bệnh được chụp ảnh phổi lần thứ nhất ngay sau khi hít khí và lần thứ hai sau đó 24,0 giờ. Biết khối lượng mol nguyên tử của xenon là 133 g/mol.