Thống kê số sản phẩm các công nhân ở tổ làm được trong một ngày được ghi lại ở bảng sau:

\[\begin{array}{|l|l|l|l|l|l|l|l|l|l|} \hline 16 & 12 & 18 & 13 & 14 & 15 & 16 & 17 & 12 & 13 \\ \hline \end{array}\]

Mẫu số liệu trên có bao nhiêu mốt?

Điểm kiểm tra Toán của tổ 1 trong lớp 10C được thống kê dưởi bảng số liệu sau:

\[\begin{array}{|l|l|l|l|l|l|l|l|l|l|} \hline 4 & 5 & 6 & 8 & 5 & 8 & 6 & 10 & 9 & 8 \\ \hline \end{array}\]

Tính khoảng tứ phân vị của mẫu số liệu trên (làm tròn kết quả đến hàng phần mười).

Phương sai là đặc trưng dùng để:

Nhiệt độ cao nhất của Hà Nội trong \(7\) ngày liên tiếp trong tháng tám được ghi lại là:

\(34;\,\,34;\,\,36;\,\,35;\,\,33;\,\,31;\,30\) (Độ C).

Độ lệch chuẩn của mẫu số liệu thuộc khoảng nào dưới đây?

Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một số sản phẩm của một số thí sinh ở bảng sau:

\[\begin{array}{|c|c|c|c|c|c|}\hline \mathbf{\text { Thời gian (phút) }} & 5 & 6 & 7 & 8 & 25 \\ \hline \mathbf{\text { Số thí sinh }} & 2 & 5 & 6 & 3 & 1 \\ \hline \end{array}\]

Giá trị ngoại lệ trong bảng trên là:

Số đặc trưng nào sau đây đo độ phân tán của mẫu số liệu?

Điểm kiểm tra Toán của tổ 1 trong lớp 10C được thống kê dưởi bảng số liệu sau:

\[\begin{array}{|l|l|l|l|l|l|l|l|l|l|} \hline 4 & 5 & 6 & 8 & 5 & 8 & 6 & 10 & 9 & 8 \\ \hline \end{array}\]

Tính độ lệch chuẩn của mẫu số liệu trên (làm tròn kết quả đến hàng phần mười).

Mẫu số liệu sau cho biết mức lương của các nhân viên trong một công ty (đơn vị: triệu đồng):

\[\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline 8 & 6 & 15 & 6 & 12 & 10 & 8 & 7 & 6 \\ \hline \end{array}\]

Hãy xác định mốt của mức lương các nhân viên trong công ty trên.

Cho mẫu số liệu thống kê sau:

\[\begin{array}{|l|l|l|l|l|} \hline 3 & 8 & 7 & 2 & 5 \\ \hline \end{array}\]

Khoảng biến thiên của mẫu số liệu trên là

Người ta thống kê độ tuổi của một số công nhân trong xí nghiệp \(B\) được cho bởi bảng tần số sau:

\[\begin{array}{|c|c|c|c|c|c|c|c|} \hline \mathbf{\text { Tuổi }} & 25 & 26 & 27 & 28 & 30 & 32 & 33 \\ \hline \mathbf{\text { Số công nhân }} & 5 & 10 & 9 & 4 & 2 & 1 & 1 \\ \hline \end{array}\]

Tìm phương sai của mẫu số liệu trong bảng trên (làm tròn đến hàng phần chục).

Để biết cây đậu phát triển như thế nào sau khi gieo hạt, bạn Châu gieo 5 hạt đậu vào 5 chậu riêng biệt và cung cấp cho chúng lượng nước, ánh sáng như nhau. Sau 2 tuần, 5 hạt đậu đã nảy mầm và phát triển thành 5 cây con. Bạn Châu đo chiều cao từ rễ đến ngọn của mỗi cây (đơn vị mm) và ghi kết quả là mẫu số liệu sau:

\[\begin{array}{|l|l|l|l|l|} \hline 112 & 102 & 106 & 94 & 101 . \\ \hline \end{array}\]

Tìm độ lệch chuẩn của các cây phát triển đồng đều? (làm tròn số thập phân thức hai)

Cuối học kì I vừa qua, bạn An đạt được kết quả sáu môn như sau:

\[\begin{array}{|c|c|} \hline \text { Môn } & \text { Điểm trung bình } \\ \hline \text { Toán } & 7,2 \\ \hline \text { Văn } & 8,0 \\ \hline \text { Anh } & 5,8 \\ \hline \text { Lý } & 7,2 \\ \hline \text { Hóa } & 9,0 \\ \hline \text { Sinh } & 4,6 \\ \hline \end{array}\]

Kết quả kiểm tra của lớp 10A được trình bày ở bảng phân bố sau đây:

\[\begin{array}{|c|c|c|c|c|c|c|c|} \hline \mathbf{\text { Điểm thi }} & 5 & 6 & 7 & 8 & 9 & 10 & \mathbf{\text { Cộng }} \\ \hline \mathbf{\text { Tần số }} & 5 & 7 & 12 & 14 & 3 & 4 & \mathbf{N=45} \\ \hline \end{array}\]

Trung vị của bảng số liệu trên bằng

Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho bởi bảng sau :

\[\begin{array}{|c|c|c|c|c|c|c|} \hline \mathbf{\text { Điểm số }} & 6 & 8 & 11 & 14 & 22 & 25 \\ \hline \mathbf{\text { Số trận }} & 1 & 2 & 5 & 5 & 3 & 4 \\ \hline \end{array}\]

Tần suất cầu thủ đó ghi được 8 điểm là:

Chiều dài (đơn vị feet) của \(7\) con cá voi trưởng thành được cho như sau:

48, 53, 51, 31, 53, 112, 52.

Số trung bình của mẫu số liệu trên là (1 feet = 0,3048 m).

Điểm thi HK1 của một học sinh lớp 10 như sau:

\[\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline 9 & 9 & 7 & 8 & 9 & 7 & 10 & 8 & 8 \\ \hline \end{array}\]

Khoảng biến thiên của mẫu số liệu là

Tìm tứ phân vị thứ ba của mẫu số liệu sau:

\[\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline 11 & 17 & 13 & 14 & 15 & 14 & 15 & 16 & 17 \\ \hline \end{array}\]

Cân nặng của 10 vận động viên môn vật của một câu lạc bộ được ghi lại ở bảng sau:

\[\begin{array}{|l|l|l|l|l|l|l|l|l|l|} \hline 56 & 57 & 68 & 63 & 67 & 65 & 56 & 66 & 67 & 69 \\ \hline \end{array}\]

Hãy xác định tứ phân vị thứ nhất của mẫu số liệu trên.

Một tổ học sinh gồm \(10\) học sinh có điểm kiểm tra cuối học kì I môn toán như sau:

\[\begin{array}{|l|l|l|l|l|l|l|l|l|l|}\hline 7 & 5 & 8 & 8 & 6 & 8 & 7 & 5 & 8 & 9\\ \hline\end{array}\]

Mốt của dãy số liệu trên là

Cuối học kì I vừa qua, bạn An đạt được kết quả sáu môn như sau:

\[\begin{array}{|c|c|} \hline \text { Môn } & \text { Điểm trung bình } \\ \hline \text { Toán } & 7,2 \\ \hline \text { Văn } & 8,0 \\ \hline \text { Anh } & 5,8 \\ \hline \text { Lý } & 7,2 \\ \hline \text { Hóa } & 9,0 \\ \hline \text { Sinh } & 4,6 \\ \hline \end{array}\]

Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

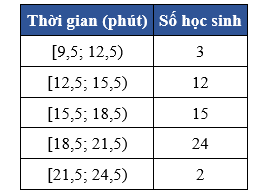
Tổng số học sinh là: