Cách 1:
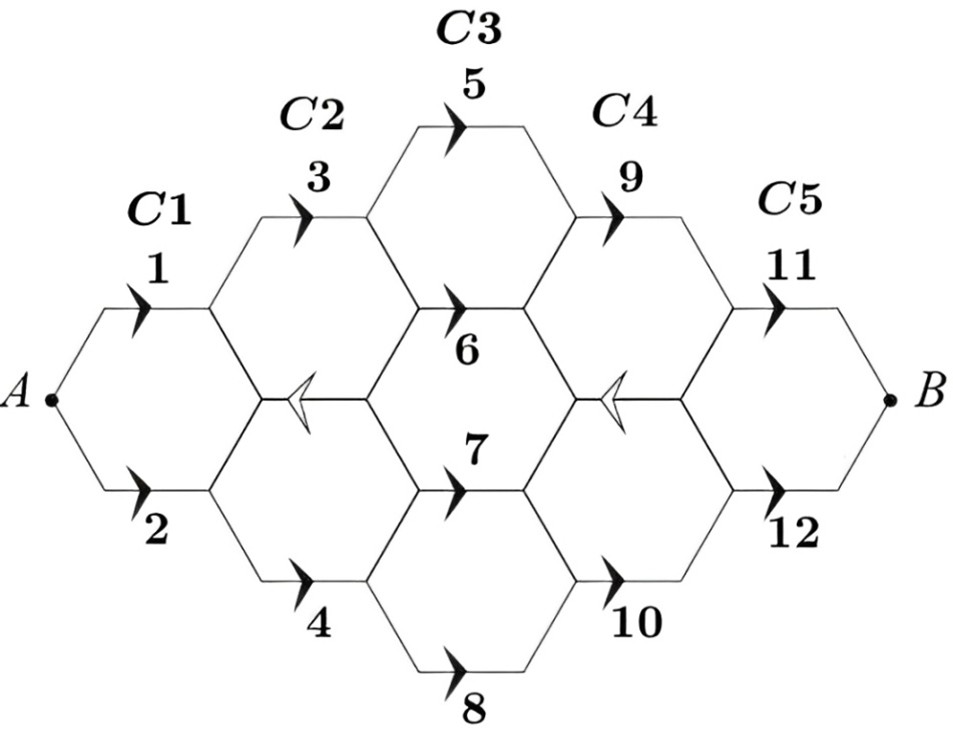
Từ A có 2 cách đến C1:
- Từ A có 1 cách đến mũi tên số 1.
- Từ A có 1 cách đến mũi tên số 2.
Từ C1 có 5 cách đến C3:
Không mất tính tổng quát giả sử đi từ C1 mũi tên số 1 đến C3 mũi tên số 6 hoặc mũi tên số 7.
- Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 6.
- Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 7.
\(\Rightarrow \) Từ C1 có 5 cách đến C3.
Từ C3 có 5 cách đến C5:
Không mất tính tổng quát giả sử đi từ C3 mũi tên số 5 đến C5 mũi tên số 11 hoặc mũi tên số 12.
- Từ mũi tên số 5 có 2 cách để đi đến mũi tên số 11.
- Từ mũi tên số 5 có 3 cách để đi đến mũi tên số 11.
\(\Rightarrow \) Từ C3 có 5 cách đến C5.
Từ C5 có 2 cách đến B:
- Từ mũi tên số 11 có 1 cách đến B.
- Từ mũi tên số 12 có 1 cách đến B.
Vậy có \(2.5.5.2=100\) cách đi từ A đến B.
Cách 2:
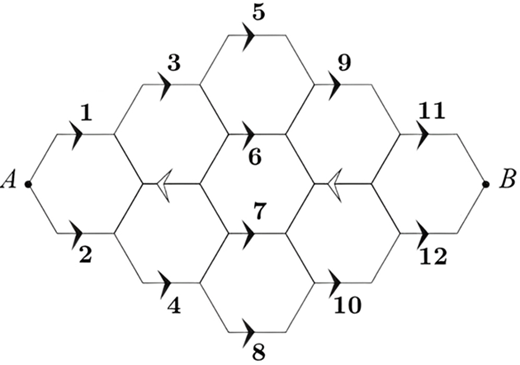
Từ A có 1 cách đi đến mũi tên 1.
- Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 5, từ mũi tên số 5 có 2 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B
\(\Rightarrow \) Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 11 và \(\text{B}\) có \(2.2=4\) cách.
- Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 6, từ mũi tên số 6 có 2 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B
\(\Rightarrow \) Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 11 và \(\text{B}\) có \(2.2=4\) cách.
- Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 7, từ mũi tên số 7 có 3 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B
\(\Rightarrow \) Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 11 và B có \(3.3=9\) cách.
- Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 8, từ mũi tên số 8 có 3 cách để đi đến mũi tên 11, từ mũi tên 11 có 1 cách đi đến B
\(\Rightarrow \) Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 11 và \(\text{B}\) có \(3.3=9\) cách.
- Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 5, từ mũi tên số 5 có 3 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B
\(\Rightarrow \) Từ mũi tên số 1 đến mũi tên số 5 rồi đến mũi tên số 12 và \(\text{B}\) có \(2.3=6\) cách.
- Từ mũi tên số 1 có 2 cách để đi đến mũi tên số 6, từ mũi tên số 6 có 3 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B
\(\Rightarrow \) Từ mũi tên số 1 đến mũi tên số 6 rồi đến mũi tên số 12 và \(\text{B}\) có \(2.3=6\) cách.
- Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 7, từ mũi tên số 7 có 2 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B
\(\Rightarrow \) Từ mũi tên số 1 đến mũi tên số 7 rồi đến mũi tên số 12 và \(\text{B}\) có \(3.2=6\) cách.
- Từ mũi tên số 1 có 3 cách để đi đến mũi tên số 8, từ mũi tên số 8 có 2 cách để đi đến mũi tên 12, từ mũi tên 12 có 1 cách đi đến B
\(\Rightarrow \) Từ mũi tên số 1 đến mũi tên số 8 rồi đến mũi tên số 12 và \(\text{B}\) có \(3.2=6\) cách.
Do đó, từ mũi tên 1 có:
\(4+4+9+9+6+6+6+6=50\) cách đi đến \(\text{B}\).
Tương tự, từ \(\text{A}\) có 1 cách đi đến mũi tên 2 và từ mũi tên 2 có 50 cách đi đến \(\text{B}\).
Vậy từ A có \(50+50=100\) cách đi đến \(\text{B}\).

















