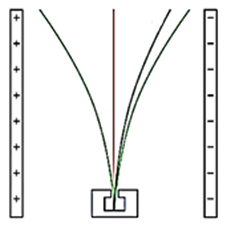
Hình bên mô tả khả năng đâm xuyên của các tia phóng xạ qua vật chất. Phát biểu nào sau đây đúng?

Chất phóng xạ pôlôni \({}_{84}^{210}Po\) phát ra tia α và biến đổi thành chì \({}_{82}^{206}Pb\). Gọi chu kì bán rã của pôlôni là T. Ban đầu (t = 0) có một mẫu \({}_{84}^{210}Po\) nguyên chất. Trong khoảng thời gian từ t = 0 đến t = 2T, có 63 mg \({}_{84}^{210}Po\) trong mẫu bị phân rã. Lấy khối lượng nguyên tử tính theo đơn vị u bằng số khối của hạt nhân của nguyên tử đó. Trong khoảng thời gian từ t = 2T đến t = 3T, lượng \({}_{82}^{206}Pb\) được tạo thành trong mẫu có khối lượng là bao nhiêu mili gam (mg)?

Trong không khí, tia phóng xạ nào sau đây có tốc độ nhỏ nhất?

Một nguồn phóng xạ ban đầu là 8.10¹⁵ Bq. Sau 10 giờ, độ phóng xạ giảm còn 1.10¹⁵ Bq.

Hằng số phóng xạ của chất phóng xạ này là bao nhiêu h-1 (làm tròn kết quả đến chữ số hàng phần trăm)?

Cho tia phóng xạ alpha \(\left( \alpha  \right)\), beta \(\left( \beta  \right)\), gamma \(\left( \gamma  \right)\) bay qua khoảng không gian giữa hai bản cực của một tụ điện được nạp điện bằng nguồn một chiều như hình bên thì

Tại một bệnh viện tuyến tỉnh, một bệnh nhân nữ 45 tuổi được chỉ định chụp PET để kiểm tra nghi ngờ di căn tuyến giáp. Do có sự chậm trễ trong quá trình vận chuyển và chuẩn bị, bệnh nhân được tiêm 1 ml dung dịch chứa đồng vị phóng xạ \({}_{\text{ }\!\!~\!\!\text{ }}^{18}\text{F}\) sau 3 giờ kể từ khi pha chế. Biết hoạt độ của mẫu tại thời điểm vừa pha chế là 150 MBq và chu kỳ bán rã của \({}_{\text{ }\!\!~\!\!\text{ }}^{18}\text{F}\) là 110 phút.

Độ phóng xạ của mẫu tại thời điểm tiêm bằng bao nhiêu MBq? (Làm tròn đến chữ số hàng đơn vị)

Poloni \({}_{84}^{210}\text{Po}\) là một chất phóng xạ α có chu kì bán rã 138 ngày và biến đổi thành hạt nhân chì \({}_{82}^{206}\text{Pb}\). Ban đầu \(\left( t~=~0 \right)\), một mẫu có khối lượng 85,0 g, trong đó 40% khối lượng của mẫu là chất phóng xạ \({}_{84}^{210}\text{Po}\), phần còn lại không có tính phóng xạ. Giả sử toàn bộ các hạt α sinh ra trong quá trình phóng xạ đều thoát ra khỏi mẫu.

Độ phóng xạ của mẫu tại thời điểm ban đầu là \(x{{.10}^{14}}\text{Bq}\). Tìm \(x\) (kết quả làm tròn đến hàng đơn vị).  

Khảo sát một mẫu đá uraninite với thành phần ban đầu chỉ gồm \({}_{92}^{238}\text{U}\). Tỉ lệ khối lượng \({}_{92}^{238}\text{U}\) còn lại và khối lượng \({}_{82}^{206}\text{Pb}\) là \(0,0453\). Chu kỳ bán rã của \({}_{92}^{238}\text{U}\) là \(4,{{5592.10}^{9}}~\text{n }\!\!\breve{\mathrm{a}}\!\!\text{ m}\). Khối lượng mol của \({}_{92}^{238}\text{U}\) là \(238\text{ }\!\!~\!\!\text{ g}/\text{mol}\), khối lượng mol của \({}_{82}^{206}\text{Pb}\) là \(206\text{ }\!\!~\!\!\text{ g}/\text{mol}\).

Tuổi của mẫu đá uraninite trên là \(z{{.10}^{10}}\text{ }\!\!~\!\!\text{ n }\!\!\breve{\mathrm{a}}\!\!\text{ m}\). Giá trị của \(z\) là bao nhiêu (làm tròn kết quả đến chữ số hàng phần trăm)?

Quy tắc nào sau đây không nên áp dụng khi làm việc với chất phóng xạ?

Dược chất phóng xạ FDG có thành phần là đồng vị \({}_{9}^{18}\text{F}\) với chu kì bán rã là 110 phút, được sử dụng trong chụp ảnh cắt lớp PET. Dược chất này được sản xuất bằng cách bắn phá vào các hạt đồng vị \({}_{8}^{18}\text{O}\) nhờ một loại hạt được tăng tốc bằng máy gia tốc. Trước khi chụp ảnh cắp lớp PET, bệnh nhân sẽ được tiêm liều lượng dược chất FDG để đảm bảo độ phóng xạ trên mỗi kg cân nặng là 0,1 mCi không đổi. Hai bệnh nhân cùng cân nặng, cùng sử dụng FDG trong cùng một đợt sản xuất, nhưng được tiêm ở 2 thời điểm cách nhau 55 phút. Bệnh nhân hai phải tiêm lượng FDG nhiều hơn bệnh nhân một bao nhiêu phần trăm (làm tròn kết quả đến hàng phần chục)?

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Trong vật lý hạt nhân, máy đo bức xạ (máy đếm/ống đếm) Geiger-Muller được sử dụng rộng rãi trong việc đo số lượng hạt \(\alpha, \beta\) bằng cách ứng dụng khả năng ion hoá của các tia bức xạ này.

Số tín hiệu máy đếm được tỉ lệ thuận với số lượng hạt nhân bị phân rã.

Xét hai máy đếm Geiger-Muller giống nhau lần lượt được chiếu xạ bởi hai mẫu chất phóng xạ \({ }_{84}^{210} \mathrm{Po}\) và \({ }_{53}^{131} \mathrm{I}\) (mỗi hạt nhân khi phân rã chỉ phát ra một tia phóng xạ). Biết rằng các mẫu chất phóng xạ được đặt ở cùng một khoảng cách so với các máy đếm tại hai phòng khác nhau. Cho khối lượng của từng mẫu phóng xạ tại thời điểm ban đầu đều là \(1,5 \mathrm{~g}\).

Lấy khối lượng của các hạt nhân gần bằng số khối của chúng; chu kì bán rã của \({ }_{84}^{210} \mathrm{Po}\) và \({ }_{53}^{131} \mathrm{I}\) lần lượt là 138,4 ngày và 8,02 ngày.

Giải thưởng Nobel Hóa học năm 1960 thuộc về Willard F.Libby (1908-1980) cho công trình nghiên cứu chất phóng xạ \({}_{6}^{14}C\), dùng để định tuổi trong khảo cổ, địa chất, địa vật lý học... Công trình nghiên cứu này bắt đầu từ 1950 khi Willard F.Libby làm việc tại Đại học Chicago, chính thức được công nhận năm 1955 và đến 1960 thì nó mang lại cho ông giải thưởng Nobel danh giá.

Khi còn sống, động thực vật tồn tại trong trạng thái cân bằng với môi trường xung quanh thông qua quá trình trao đổi carbon với khí quyển hoặc thông qua chế độ hấp thụ dinh dưỡng của chúng. Do vậy, lượng \({}_{6}^{14}C\) trong chúng có tương quan với lượng \({}_{6}^{14}C\) khí quyển. Để xác định tuổi của một mẫu gỗ cổ, các nhà nghiên cứu nhận thấy khi cây gỗ chết, lượng \({}_{6}^{14}C\)trong thân cây bị phân rã với chu kỳ 5730 năm. Tại thời điểm khảo sát mẫu gỗ cổ, các nhà nghiên cứu nhận thấy lượng \({}_{6}^{14}C\)chỉ bằng một phần ba lượng \({}_{6}^{14}C\)trong mẫu gỗ tương đương đang còn sống.

Theo một lí thuyết của các nhà thiên văn học thì các nguyên tố nặng có trên các hành tinh trong vũ trụ được tạo ra từ các vụ nổ siêu tân tinh (cái chết của một ngôi sao nặng). Cho rằng \({}_{{}}^{235}U\) và \({}_{{}}^{238}U\) được tạo ra từ mỗi vụ nổ siêu tân tinh đều có cùng số nguyên tử. Hiện nay, tỉ số về số nguyên tử giữa \({}_{{}}^{235}U\) với \({}_{{}}^{238}U\) trên Trái Đất là 0,00725. Biết \({}_{{}}^{235}U\) và \({}_{{}}^{238}U\) là các chất phóng xạ với chu kì bán rã lần lượt là 0,704 tỉ năm và 4,47 tỉ năm. Số avôgađrô là NA = 6,02.1023 mol^-1.

Radon là khí không màu, không mùi và không vị. Do đó không thể phát hiện chỉ bằng giác quan con người. Radon \(_{86}^{222}Rn\) là một đồng vị phân rã alpha và sinh ra hạt nhân con X với chu kỳ 3,82 ngày. Nguyên tố \(_{86}^{222}Rn\) tích tụ trong các ngôi nhà được WHO cho là nguyên nhân thứ hai gây ra bệnh ung thư phổi sau thuốc lá. Trong một khảo sát tại Bình Dương, Việt Nam người ta đo được độ phóng xạ trong 1m³ không khí chứa khoảng 11,4 triệu nguyên tử khí radon. Biết rằng độ phóng xạ an toàn của radon trong không khí vào khoảng 150 Bq/m³.

Biển báo sau đây mang ý nghĩa

Đồng vị mendelevium \({ }^{258}{ }_{101} \mathrm{Md}\) là chất phóng xạ \(\alpha\) có chu kì bán rã 51,5 ngày và khối lượng ban đầu là 105 g . Cho biết khối lượng của các hạt \({ }^{258}{ }_{101} \mathrm{Md},{ }^{4} \mathrm{He}\), và hạt sản phẩm lần lượt là \(258,0984 \mathrm{u} ; 4,0026 \mathrm{u}\); và \(254,0880 \mathrm{u}\). Năng lượng toả ra của phản ứng phân rã phóng xạ trên là \(7,27 \mathrm{MeV}\).

Đồng vị phóng xạ \({ }_{84}^{210} \mathrm{Po}\) có chu kì bán rã là 138,4 ngày. Xét một mẫu chất đang chứa \(\mathrm{N}_{0}\) hạt nhân \({ }_{84}^{210} \mathrm{Po}\) (tại thời điểm ban đầu). Sau bao lâu kể từ thời điểm ban đầu thì tỉ số giữa số hạt nhân \({ }_{84}^{210} \mathrm{Po}\) đã phân rã thành hạt nhân khác và số hạt nhân \({ }_{84}^{210} \mathrm{Po}\) còn lại bằng 3 ?

Potassium là nguyên tố dinh dưỡng khoáng thiết yếu đối với cây trồng. Trong potassium tự nhiên có 0,0117% là đồng vị phóng xạ \(_{19}^{40}K\) với chu kì bán rã là 1,25.10⁹ năm.

Độ phóng xạ của \(_{19}^{40}K\) trong mỗi gam potassium tự nhiên là bao nhiêu Bq (làm tròn kết quả đến chữ số hàng đơn vị)?

Ngày 12/9/2014, một sự cố nghiêm trọng xảy ra tại TP.HCM khi Công ty TNHH Apave Châu Á – Thái Bình Dương báo cáo bị thất lạc một thiết bị chứa nguồn phóng xạ Iridium -\({}_{\text{ }\!\!~\!\!\text{ }}^{192}\text{Ir}\) dùng trong kiểm tra mối hàn công nghiệp. Theo hồ sơ ghi nhận vào thời điểm bàn giao thiết bị, nguồn \({}_{\text{ }\!\!~\!\!\text{ }}^{192}\text{Ir}\) có khối lượng ban đầu 5,0 g, được cất giữ trong một thiết bị bọc chì chuyên dụng. Chu kỳ bán rã của \({}_{\text{ }\!\!~\!\!\text{ }}^{192}\text{Ir}\) là khoảng 74 ngày và mỗi phân rã phát ra tia gamma mạnh. Một năm sau sự cố, các nhà chức trách tiến hành rà soát lại các thiết bị còn tồn đọng, đồng thời đo hoạt độ còn lại để xác định mức độ nguy hiểm.

Ước tính rằng 2,42.10²³ phân tử MIC tạo thành một liều lượng nguy hiểm cho con người, số lượng người tối đa có thể bị đe dọa bởi lượng MIC còn lại trong khoang chứa là bao nhiêu?

 Chất phóng xạ \(_{}^{25}Na\) có chu kì bán rã 62 s.

Độ phóng xạ của 0,248 mg \(_{}^{25}Na\) là X.10¹⁶ Bq. Tìm X (làm tròn kết quả đến chữ số hàng phần trăm).

Một mẫu phóng xạ \({}_{88}^{226}\text{Ra}\) có chu kì bán rã là 1600 năm. Ban đầu \(\left( t=0 \right)\), mẫu \({}_{88}^{226}\text{Ra}\) tinh khiết có khối lượng 10 g. Sau 4800 năm, khối lượng chất phóng xạ \({}_{88}^{226}\text{Ra}\) còn lại trong mẫu này là