Câu hỏi:
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(y=\frac{8}{3} x^{3}+2 \ln x-m x\) đồng biến trên \((0 ; 1)\) ?
Đáp án đúng: B
ТХĐ: \(D=\mathbb{R}\).
Ta có \(y^{\prime}=8 x^{2}+\frac{2}{x}-m\). Yêu cầu bài toán \(\Leftrightarrow y^{\prime} \geq 0 ~\forall x \in(0 ; 1)\)
\(\Leftrightarrow 8 x^{2}+\frac{2}{x}-m \geq 0 ~\forall x \in(0 ; 1) \Leftrightarrow h(x)=8 x^{2}+\frac{2}{x} \geq m ~\forall x \in(0 ; 1) \Leftrightarrow m \leq \min _{(0 ; 1)} h(x)\).
Xét hàm \(h(x)=8 x^{2}+\frac{2}{x} ~\forall x \in(0 ; 1)\). Ta có \(h^{\prime}(x)=16 x-\frac{2}{x^{2}} \Rightarrow h^{\prime}(x)=0 \Rightarrow x=\frac{1}{2}\).
Bảng biến thiên
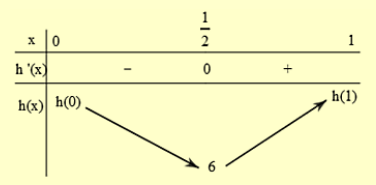
Từ \(\mathrm{BBT} \Rightarrow m \leq 6\), kết hợp với \(m\) nguyên dương ta được \(m \in\{1 ; 2 ; 3 ; 4 ; 5 ; 6\}\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026

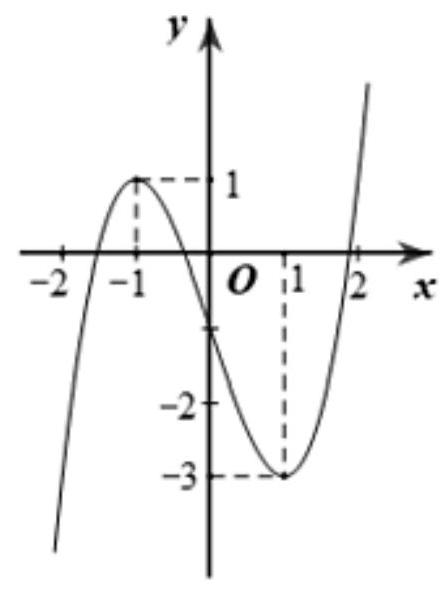
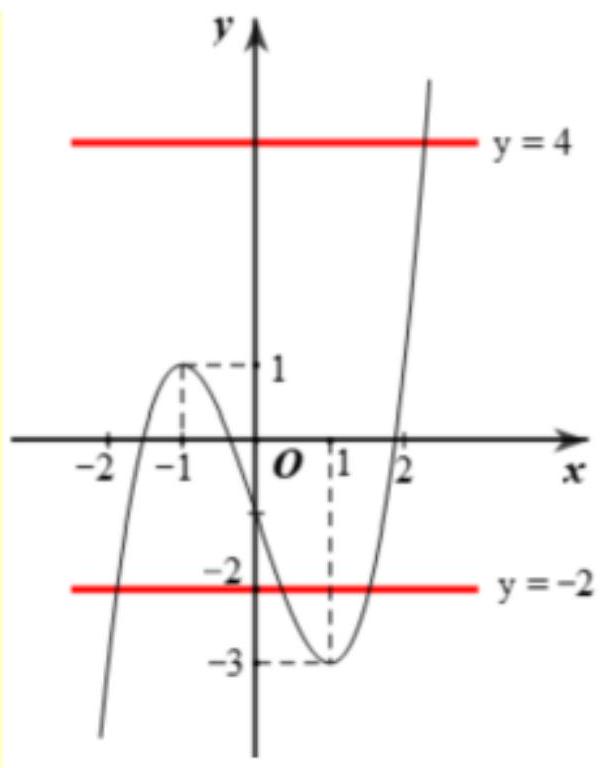
 Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)
Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)