Câu hỏi:
Cho tập \(S=\{1 ; 2 ; \ldots ; 19 ; 20\}\) gồm 20 số tự nhiên từ 1 đến 20. Lấy ngẫu nhiên ba số thuộc \(S\). Xác suất để ba số lấy được lập thành cấp số cộng là
Đáp án đúng: C
Ta có: \(n(\Omega)=C_{20}^{3}\).
Gọi A là biến cố. "ba số lấy được lập thành cấp số cộng".
Giả sử ba số \(a, b, c\) theo thứ tự đó lập thành cấp số cộng, khi đó ta có \(a+c=2 b\). Hay \(a+c\) là một số chẵn và mỗi cách chọn 2 số \(a\) và \(c\) thỏa mãn \(a+c\) là số chẵn sẽ có duy nhất cách chọn Số cách chọn hai số có tổng chẵn sẽ là số cách chọn ba số tạo thành cấp số cộng.
TH1. Hai số lấy được đều là số chẵn, có: \(C_{10}^{2}\) cách lấy.
TH2. Hai số lấy được đều là số lẻ, có: \(C_{10}^{2}\) cách lấy.
\(\Rightarrow n(A)=C_{10}^{2}+C_{10}^{2}\)
\(P(A)=\frac{n(A)}{n(\Omega)}=\frac{C_{10}^{2}+C_{10}^{2}}{C_{10}^{3}}=\frac{3}{38}\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026

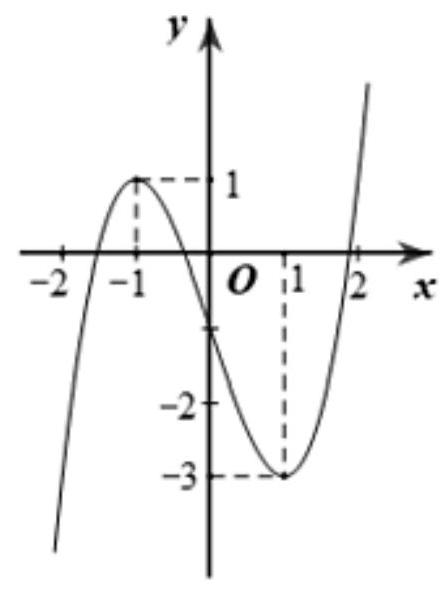
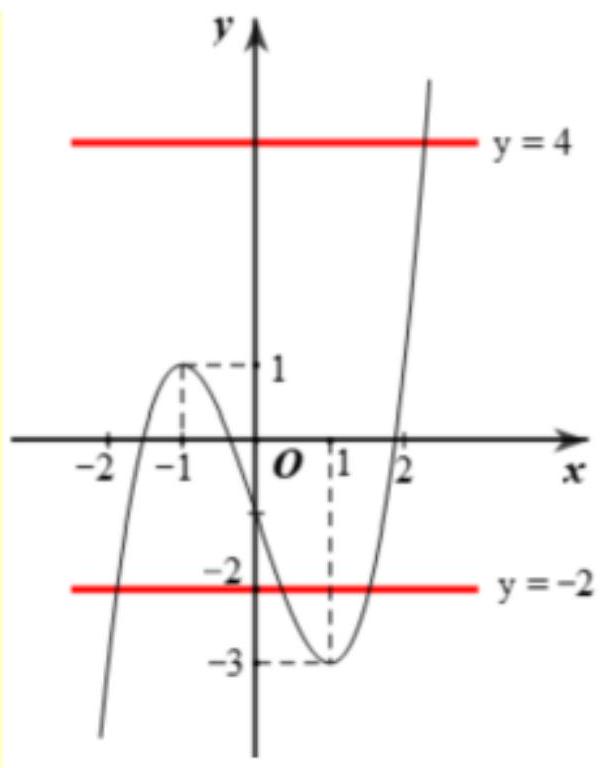
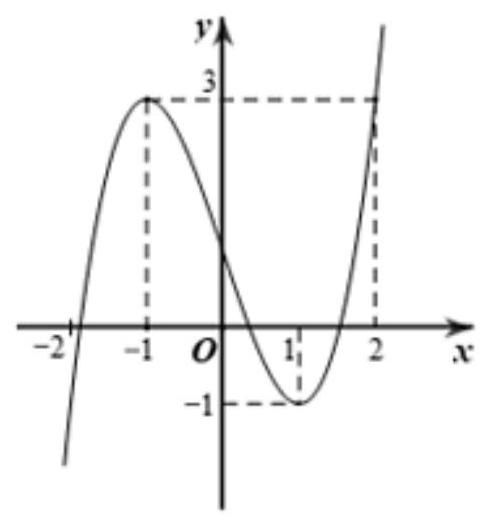 Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)
Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)