Câu hỏi:
Cho tứ diện đều \(A B C D\) có độ dài các cạnh bằng \(2 a\). Gọi \(M, N\) lần lượt là trung điểm các cạnh \(A C, B C ; P\) là trọng tâm tam giác \(B C D\). Mặt phẳng \((M N P)\) cắt tứ diện theo một thiết diện có diện tích là
Đáp án đúng: C
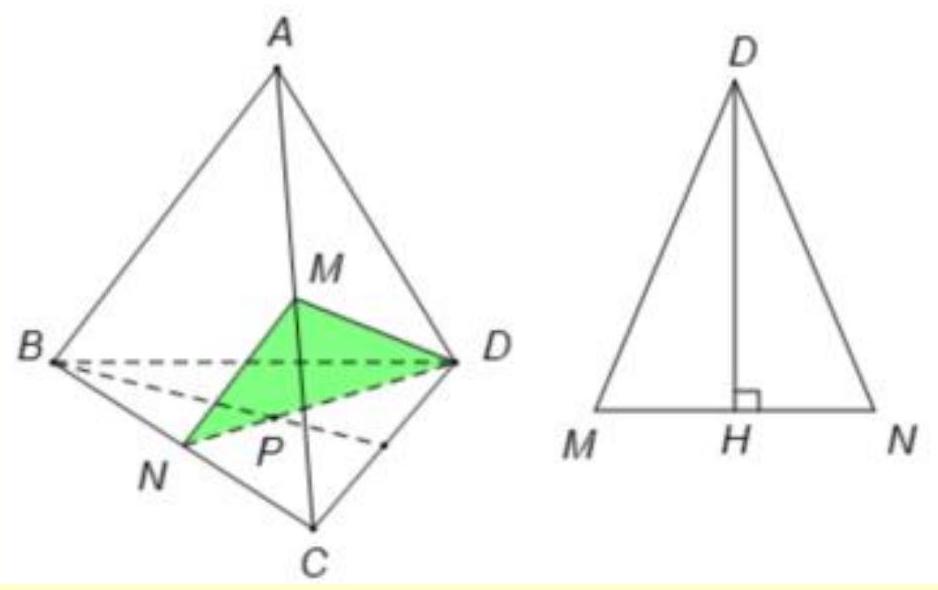
Trong tam giác \(B C D\) có: \(P\) là trọng tâm, \(N\) là trung điểm \(B C\). Suy ra \(N, P, D\) thẳng hàng.
Vậy thiết diện là tam giác \(M N D\)
Xét tam giác \(M N D\), ta có \(M N=\frac{A B}{2}=a ; D M=D N=\frac{A D \sqrt{3}}{2}=a \sqrt{3}\).
Do đó tam giác \(M N D\) cân tại \(D\).
Gọi \(H\) là trung điểm \(M N\) suy ra \(D H \perp M N\).
Diện tích tam giác \(S_{\triangle M N D}=\frac{1}{2} M N. D H=\frac{1}{2} M N. \sqrt{D M^{2}-M H^{2}}=\frac{a^{2} \sqrt{11}}{4}\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026

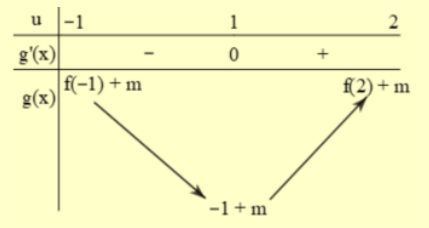
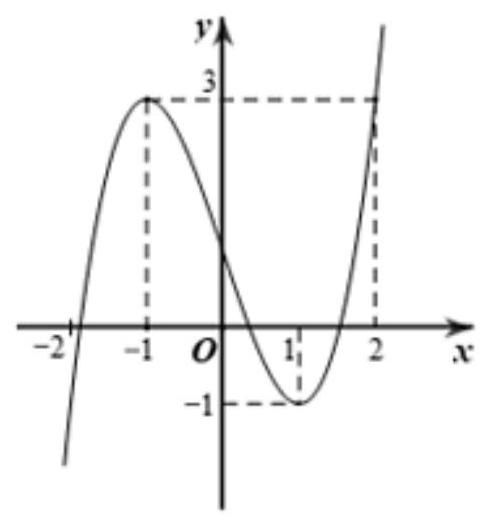 Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)
Xét hàm số \(g(x)=f\left(2 x^{3}+x-1\right)+m\). Với giá trị nào của \(m\) thì giá trị nhỏ nhất của \(g(x)\) trên đoạn \([0;1]\) bằng \(- 20\)