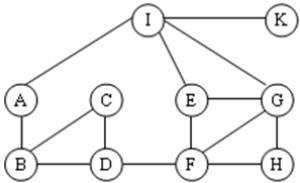
Với đồ thị n đỉnh, độ phức tạp tính toán của thuật toán Dijkstra là:
Đáp án đúng: D
Thuật toán Dijkstra được sử dụng để tìm đường đi ngắn nhất từ một đỉnh nguồn đến tất cả các đỉnh còn lại trong một đồ thị có trọng số không âm. Độ phức tạp của thuật toán Dijkstra phụ thuộc vào cách cài đặt:
- Nếu sử dụng mảng để tìm đỉnh có khoảng cách ngắn nhất, độ phức tạp là O(n2), trong đó n là số đỉnh.
- Nếu sử dụng hàng đợi ưu tiên (ví dụ: heap nhị phân) để tìm đỉnh có khoảng cách ngắn nhất, độ phức tạp là O((m+n) log n), trong đó m là số cạnh và n là số đỉnh. Với đồ thị dày đặc, m có thể là O(n2), khi đó độ phức tạp gần với O(n2 log n). Với đồ thị thưa, m gần với O(n), thì độ phức tạp gần với O(n log n).
Trong các đáp án đã cho, O(n2 log2n) thể hiện độ phức tạp khi sử dụng hàng đợi ưu tiên (heap) và thường được chấp nhận là độ phức tạp phổ biến của thuật toán Dijkstra.
Bộ 525 câu hỏi trắc nghiệm ôn thi môn Toán rời rạc có đáp án dưới đây sẽ là tài liệu ôn tập hữi ích dành cho các bạn sinh viên. Mời các bạn cùng tham khảo!
Câu hỏi liên quan
Thuật toán BFS (Breadth-First Search) duyệt đồ thị theo chiều rộng. Bắt đầu từ đỉnh I, ta duyệt các đỉnh kề với I trước, sau đó duyệt các đỉnh kề với các đỉnh vừa duyệt, cứ tiếp tục như vậy cho đến khi duyệt hết các đỉnh có thể đến được từ I.
1. Bắt đầu từ đỉnh I.
2. Các đỉnh kề với I là A và B. Ta duyệt A trước (vì A đứng trước B theo thứ tự chữ cái).
3. Các đỉnh kề với A là E và G. Ta duyệt E trước.
4. Các đỉnh kề với E là K. Ta duyệt K.
5. Tiếp theo, quay lại duyệt các đỉnh kề với I (đã duyệt A), ta duyệt B.
6. Các đỉnh kề với B là C và F. Ta duyệt C trước.
7. Các đỉnh kề với C là H. Ta duyệt H.
8. Tiếp theo, quay lại duyệt các đỉnh kề với B (đã duyệt C), ta duyệt F.
9. Các đỉnh kề với F là D. Ta duyệt D.
Vậy thứ tự duyệt các đỉnh là: I, A, E, G, K, B, C, F, H, D
Biểu thức hội cơ bản (minterm) là một biểu thức logic được tạo thành bằng cách kết hợp các biến mệnh đề hoặc phủ định của chúng bằng phép toán AND (phép hội). Mỗi biến xuất hiện một lần trong biểu thức, hoặc ở dạng khẳng định, hoặc ở dạng phủ định.
Do đó, đáp án đúng là:
\(F = {q_1} \wedge {q_2} \wedge ... \wedge {q_n}\) với qj = pj hoặc \({q_j} = \overline {{p_j}} (j = 1,...,n)\)
Trong các phương án đã cho, chỉ có phương án 3 thể hiện đúng cấu trúc của một biểu thức hội (AND). Phương án 1 và 2 sử dụng phép tuyển (OR), không phải phép hội (AND).
Ta có X = 0, Y = 0, Z = 1. Thay vào biểu thức (\(\neg \)X→Y ) \(\wedge \) (\(\neg \)Y → Z ) và (\(\neg \)X →Z) như sau:
- (\(\neg \)X→Y ) \(\wedge \) (\(\neg \)Y → Z ) = (\(\neg \)0 → 0) \(\wedge \) (\(\neg \)0 → 1) = (1 → 0) \(\wedge \) (1 → 1) = 0 \(\wedge \) 1 = 0
- (\(\neg \)X →Z) = (\(\neg \)0 → 1) = (1 → 1) = 1
Vậy, chân trị của biểu thức là 0 và 1.
Để giải quyết câu hỏi này, chúng ta cần xem xét tính đúng sai của từng biểu thức logic Boole:
- X + 0 = X: Biểu thức này đúng, vì phép OR (tức là '+') với 0 không ảnh hưởng đến giá trị của X.
- X + 1 = X: Biểu thức này; sai. Vì phép OR với 1 luôn cho kết quả là 1, bất kể giá trị của X là gì. Do đó, X + 1 = 1 chứ không phải là X.
- X + (Y + Z) = (X + Y) + Z = X + Y + Z: Biểu thức này đúng, thể hiện tính kết hợp của phép OR.
- (W + X)(Y + Z) = WY + XY + WZ + XZ: Biểu thức này đúng, nó tuân theo quy tắc phân phối của phép AND (nhân) đối với phép OR (cộng).
Vậy, biểu thức sai là X + 1 = X.
