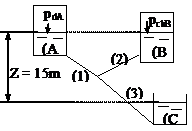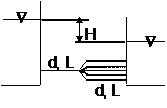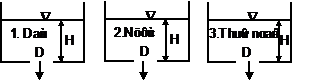Bể chứa dầu có cột dầu cao 4m không đổi. Vận tốc lý thuyết (bỏ qua tổn thất) của dầu chảy qua lỗ ở đây là:

Công thức tính lưu lượng qua lỗ mỏng là: Q = μ * S * √(2gH), trong đó:
- Q là lưu lượng (m³/s)
- μ là hệ số lưu lượng
- S là diện tích lỗ (m²)
- g là gia tốc trọng trường (≈ 9.81 m/s²)
- H là cột áp (m)

Trong bài này:
- μ = 0.6
- S = 5 cm² = 5 * 10⁻⁴ m²
- H = 4 m
- g ≈ 9.81 m/s²

Thay số vào công thức:
Q = 0.6 * 5 * 10⁻⁴ * √(2 * 9.81 * 4) ≈ 0.6 * 5 * 10⁻⁴ * √78.48 ≈ 0.6 * 5 * 10⁻⁴ * 8.8589 ≈ 2.65767 * 10⁻³ m³/s

Đổi sang lit/s: 2.65767 * 10⁻³ m³/s * 1000 lit/m³ ≈ 2.66 lit/s

Vậy đáp án đúng là 2,66 lit/s.

Áp dụng phương trình Bernoulli giữa mặt thoáng bể lớn và mặt thoáng đầu ra của ống:
P1/γ + V1^2/2g + Z1 = P2/γ + V2^2/2g + Z2 + h_loss

Trong đó:
- P1 = P2 = P_atm (áp suất khí quyển)
- V1 ≈ 0 (vận tốc mặt thoáng bể lớn coi như bằng 0)
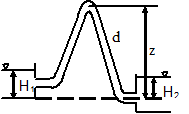
- Z1 - Z2 = H1 = 3.5m
- h_loss = h_vào = 0.5m

Vậy:
H1 = V2^2/2g + H2 + h_loss

Vì không có tổn thất dọc đường và cục bộ khác ngoài tổn thất vào, ta có:
3. 5 = V2^2/2g + H2 + 0.5

Vì đầu ra là mặt thoáng nên V2 ≈ 0 (vận tốc dòng chảy tại đầu ra coi như không đáng kể so với vận tốc trong ống), ta có:
3. 5 = H2 + 0.5

=> H2 = 3.5 - 0.5 = 3m

Gọi Q1 là lưu lượng ban đầu, Q2 là lưu lượng sau khi nối ống.

Áp dụng công thức Darcy-Weisbach cho đoạn ống ban đầu:
ΔH = (λ * (2L) / d) * (v1^2 / (2g))

Với v1 = Q1 / A, A là diện tích mặt cắt ngang của ống.

Khi nối 4 ống song song, lưu lượng qua mỗi ống là Q2/4. Áp dụng công thức Darcy-Weisbach cho một trong 4 nhánh song song:
ΔH = (λ * L / d) * (v2^2 / (2g))

Với v2 = (Q2/4) / A

Vì độ chênh áp ΔH là như nhau, ta có:
(λ * (2L) / d) * (v1^2 / (2g)) = (λ * L / d) * (v2^2 / (2g))

Thay v1 và v2 vào:
(2L / d) * (Q1/A)^2 = (L / d) * ((Q2/4) / A)^2

2 * Q1^2 = (Q2^2) / 16

Q2^2 = 32 * Q1^2

Q2 = Q1 * √32 = Q1 * √(16*2) = 4√2 * Q1 ≈ 5.66 * Q1

Tuy nhiên, ở đây ta có 4 nhánh song song dài L. Tổn thất trên đoạn ống 2L ban đầu bằng tổng tổn thất trên 1 nhánh chiều dài L và tổn thất trên đoạn L còn lại. Do đó:
H = (λ * L / d) * (v1^2 / (2g)) + (λ * L / d) * (v1^2 / (2g)) = (λ * L / d) * (v2^2 / (2g))
2*(λ * L / d) * (v1^2 / (2g)) = (λ * L / d) * (v2^2 / (2g))
2*(Q1/A)^2 = ((Q2/4)/A)^2
2*Q1^2 = Q2^2/16
Q2^2 = 32*Q1^2
Q2 = sqrt(32)*Q1 = 4*sqrt(2)*Q1 = 5.656*Q1
Tổng lưu lượng Q = 4*Q_nhánh = 4*1.414*Q1 = 5.656Q1
Đề bài có lẽ bị nhầm lẫn ở chỗ nối 4 nhánh song song dài L, đường kính d ở giữa ống.
Nếu bỏ qua đoạn ống L ban đầu, và chỉ tính 4 nhánh song song thì làm như sau:
Tổn thất áp suất trên ống ban đầu là:
H = (λ * 2L / d) * (Q1/A)^2
Sau khi nối 4 ống song song, tổn thất áp suất trên mỗi ống là:
H = (λ * L / d) * ((Q2/4)/A)^2
Suy ra: (λ * 2L / d) * (Q1/A)^2 = (λ * L / d) * ((Q2/4)/A)^2
2Q1^2 = (Q2/4)^2 * L/L
Q2^2 = 32Q1^2
Q2 = 4√2Q1 ≈ 5.66Q1
Vì có 4 nhánh song song nên lưu lượng tăng lên 5.66/4 lần. Vậy không có đáp án đúng ở đây.
Nếu như câu hỏi là tính tổng lưu lượng qua 4 ống thì đáp án sẽ là khoảng 5.66 lần, không có đáp án đúng.
Nếu như câu hỏi là tính lưu lượng qua MỘT ống trong 4 ống thì ta sẽ có Q2/4 = 1.414Q1 => tăng 1.414 lần, cũng không có đáp án đúng.
Có lẽ đề bài muốn hỏi tổng lưu lượng tăng lên bao nhiêu lần khi có 4 ống song song, bỏ qua đoạn ống L phía trước. Khi đó áp suất giảm 1 nửa và có:
H = (λ * 2L / d) * (v1^2 / (2g))
H/2 = (λ * L / d) * (v2^2 / (2g))
=> Q2=2*Q1 => Lưu lượng qua 1 ống tăng 2 lần. Do có 4 ống => Tổng lưu lượng tăng 2*4 = 8 lần.
Nhưng đề bài cho đáp án rất lạ.

Do đó câu này không có đáp án đúng.

Thời gian để tháo hết chất lỏng phụ thuộc vào vận tốc dòng chảy ra khỏi lỗ. Vận tốc này phụ thuộc vào áp suất tại lỗ, mà áp suất này phụ thuộc vào độ cao cột chất lỏng và khối lượng riêng của chất lỏng. Vì độ cao H như nhau, chất lỏng có khối lượng riêng càng lớn thì áp suất tại lỗ càng lớn, vận tốc dòng chảy càng lớn và thời gian tháo hết càng nhỏ. Thủy ngân có khối lượng riêng lớn nhất, sau đó đến nước và cuối cùng là dầu. Do đó, T1 > T2 > T3.