Trả lời:
Đáp án đúng: C
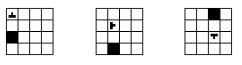
Quan sát các hình ảnh được cung cấp, ta có thể nhận thấy một quy luật xoay vòng của các hình tam giác và hình tròn. Ở hình đầu tiên, có một hình tam giác nằm trên một hình tròn. Sang hình thứ hai, hình tam giác di chuyển sang phải và hình tròn vẫn giữ nguyên vị trí. Ở hình thứ ba, hình tam giác lại di chuyển xuống dưới và hình tròn vẫn giữ nguyên. Vì vậy, theo quy luật này, ở hình tiếp theo, hình tam giác sẽ di chuyển sang trái, trong khi hình tròn vẫn giữ nguyên vị trí. Phương án thứ tư (đáp án số 3) thể hiện đúng quy luật này với hình tam giác nằm bên trái hình tròn.
Câu hỏi liên quan
Lời giải:
Đáp án đúng: A
Câu hỏi yêu cầu xác định hình X dựa trên các tiêu chí sau:
1. Hình X được lặp lại 2 lần trong ma trận.
2. Hình X thuộc cột C3.
3. Hình X thuộc dòng L2.
4. Hình X không thuộc cột C1.
Ta quan sát ma trận hình:
* Cột C3: Bao gồm các hình ở vị trí (L1, C3), (L2, C3), (L3, C3).
* Dòng L2: Bao gồm các hình ở vị trí (L2, C1), (L2, C2), (L2, C3).
Kết hợp hai điều kiện 'thuộc cột C3' và 'thuộc dòng L2', ta xác định được hình X phải nằm ở vị trí giao nhau là (L2, C3).
Bây giờ, ta xem xét hình ở vị trí (L2, C3). Đó là hình chữ nhật có dấu chấm ở giữa.
Tiếp theo, ta kiểm tra các điều kiện còn lại với hình này:
* Hình lặp lại 2 lần: Quan sát toàn bộ ma trận, hình chữ nhật có dấu chấm ở giữa xuất hiện ở vị trí (L2, C3) và (L3, C1). Vậy hình này lặp lại đúng 2 lần.
* Không thuộc cột C1: Hình này ở cột C3 nên không thuộc cột C1.
Các tiêu chí đều được thỏa mãn với hình chữ nhật có dấu chấm ở giữa, nằm ở vị trí (L2, C3). Hình này tương ứng với phương án A.
Do đó, đáp án đúng là A.
1. Hình X được lặp lại 2 lần trong ma trận.
2. Hình X thuộc cột C3.
3. Hình X thuộc dòng L2.
4. Hình X không thuộc cột C1.
Ta quan sát ma trận hình:
* Cột C3: Bao gồm các hình ở vị trí (L1, C3), (L2, C3), (L3, C3).
* Dòng L2: Bao gồm các hình ở vị trí (L2, C1), (L2, C2), (L2, C3).
Kết hợp hai điều kiện 'thuộc cột C3' và 'thuộc dòng L2', ta xác định được hình X phải nằm ở vị trí giao nhau là (L2, C3).
Bây giờ, ta xem xét hình ở vị trí (L2, C3). Đó là hình chữ nhật có dấu chấm ở giữa.
Tiếp theo, ta kiểm tra các điều kiện còn lại với hình này:
* Hình lặp lại 2 lần: Quan sát toàn bộ ma trận, hình chữ nhật có dấu chấm ở giữa xuất hiện ở vị trí (L2, C3) và (L3, C1). Vậy hình này lặp lại đúng 2 lần.
* Không thuộc cột C1: Hình này ở cột C3 nên không thuộc cột C1.
Các tiêu chí đều được thỏa mãn với hình chữ nhật có dấu chấm ở giữa, nằm ở vị trí (L2, C3). Hình này tương ứng với phương án A.
Do đó, đáp án đúng là A.
Lời giải:
Đáp án đúng: a
Hình ảnh hiển thị một dãy các chữ cái: A, C, F, J, ?. Dựa trên quy luật của dãy số, ta nhận thấy khoảng cách giữa các chữ cái liên tiếp tăng dần: từ A đến C là 2 (A + 2 = C), từ C đến F là 3 (C + 3 = F), từ F đến J là 4 (F + 4 = J). Theo quy luật này, chữ cái tiếp theo sẽ là J + 5. Chữ cái thứ 10 trong bảng chữ cái là J, cộng thêm 5 sẽ ra chữ cái thứ 15, đó là chữ O. Tuy nhiên, các phương án đưa ra không có chữ O. Chúng ta cần xem xét lại quy luật. Một quy luật khác có thể là vị trí của các chữ cái trong bảng chữ cái: A (1), C (3), F (6), J (10). Hiệu số giữa các số thứ tự này là: 3-1=2, 6-3=3, 10-6=4. Quy luật này tương tự như trên, và số tiếp theo sẽ là 10+5=15. Chữ cái thứ 15 là O. Nếu vẫn không có trong đáp án, ta xem xét quy luật khác. Có thể câu hỏi có lỗi hoặc hình ảnh không hiển thị rõ. Tuy nhiên, nếu nhìn kỹ vào hình ảnh, các chữ cái được sắp xếp theo một kiểu hình học đặc biệt. Chữ cái A ở đỉnh, hai chữ C ở hai bên, hai chữ F ở hàng dưới, và hai chữ J ở hàng cuối cùng. Dựa trên cách sắp xếp này, có thể chữ cái còn thiếu sẽ nằm ở vị trí tương tự như các chữ cái khác trong hàng cuối cùng. Tuy nhiên, quy luật hình học này không rõ ràng và không có phương án nào gợi ý rõ ràng. Quay lại quy luật số thứ tự, nếu có sai sót trong việc đếm hoặc diễn giải, ta cần xem lại. Nếu các phương án là G, H, E, P, ta thử xem xét nếu chữ cái còn thiếu là một trong số đó. Nếu là G (7), khoảng cách từ J (10) là 3. Nếu là H (8), khoảng cách là 2. Nếu là E (5), khoảng cách là -5. Nếu là P (16), khoảng cách là 6. Quy luật tăng dần 2, 3, 4, 5 đã được xem xét và cho ra O. Có thể có một cách nhìn khác. Ta hãy giả định rằng câu hỏi và các phương án đều đúng và có một quy luật nhất quán. Hãy thử nghĩ đến các dãy số liên quan đến hình học hoặc các quy luật khác. Tuy nhiên, với thông tin hiện có, quy luật tăng dần khoảng cách là hợp lý nhất. Nếu xét đến các phương án đã cho, có khả năng quy luật không phải là tăng dần 2, 3, 4, 5. Hãy xem xét lại hình ảnh. Có thể hình ảnh được thiết kế để tạo ra một chữ cái. Nếu chữ cái còn thiếu là E, thì dãy có thể là A, C, E, ?, J. Khoảng cách là 2, 2, ?, ?. Nếu khoảng cách đều là 2, thì sẽ là A, C, E, G, I. Không khớp. Hãy xem xét lại quy luật tăng dần khoảng cách. A (1), C (3), F (6), J (10). Hiệu: 2, 3, 4. Số tiếp theo trong dãy hiệu là 5. Vậy số thứ tự là 10 + 5 = 15, tương ứng với chữ O. Vì O không có trong các đáp án, ta cần tìm một quy luật khác hoặc nhận định rằng câu hỏi có vấn đề. Tuy nhiên, vì phải chọn một đáp án, ta sẽ tìm quy luật nào dẫn đến các đáp án có sẵn. Nếu giả sử chữ còn thiếu là G (7), thì dãy hiệu là 2, 3, 4, -3. Không hợp lý. Nếu là H (8), dãy hiệu là 2, 3, 4, -2. Không hợp lý. Nếu là E (5), dãy hiệu là 2, 3, 4, -5. Không hợp lý. Nếu là P (16), dãy hiệu là 2, 3, 4, 6. Đây có thể là một quy luật khác: hiệu số tăng dần 2, 3, 4, 6. Tuy nhiên, sự nhảy vọt từ 4 lên 6 không tuân theo quy luật tăng đều. Trong trường hợp này, một khả năng khác là quy luật không phải là dựa trên vị trí trong bảng chữ cái mà dựa trên một hình ảnh hoặc một cấu trúc nhất định. Tuy nhiên, không có thông tin bổ sung. Nếu xét theo quy luật tăng dần hiệu số 2, 3, 4, 5 cho ra O. Với các phương án A, C, F, J, và các lựa chọn G, H, E, P. Giả sử câu hỏi có lỗi đánh máy và chữ F thực ra là D. Thì dãy là A(1), C(3), D(4), J(10). Hiệu: 2, 1, 6. Không hợp lý. Quay lại quy luật ban đầu với A(1), C(3), F(6), J(10). Hiệu số là 2, 3, 4. Nếu số tiếp theo là 5 thì ta có O. Nếu ta phải chọn một trong các đáp án, có thể có một quy luật phức tạp hơn hoặc một lỗi trong câu hỏi/đáp án. Tuy nhiên, trong các bài tập dạng này, quy luật tăng dần khoảng cách là phổ biến nhất. Nếu câu hỏi yêu cầu tìm chữ còn thiếu để hoàn thành một hình dạng hoặc một pattern, và quy luật số học không cho kết quả trong các lựa chọn. Hãy xem xét lại hình ảnh một lần nữa. Hình ảnh hiển thị các chữ cái được sắp xếp đối xứng. A ở trên cùng. Hai chữ C hai bên A. Hai chữ F dưới C. Hai chữ J dưới F. Nếu quy luật là đối xứng và tăng dần xuống dưới, thì hàng cuối cùng có thể có hai chữ cái. Tuy nhiên, chỉ có một chỗ trống. Nếu ta nhìn theo cột, thì không có quy luật rõ ràng. Nếu ta nhìn theo hàng ngang, thì có quy luật tăng dần khoảng cách. A, C, F, J. Hiệu 2, 3, 4. Nếu ta phải chọn một chữ cái từ G, H, E, P. Có thể chữ cái còn thiếu là P. Khoảng cách từ J (10) đến P (16) là 6. Như vậy, dãy hiệu số sẽ là 2, 3, 4, 6. Đây là một khả năng, mặc dù quy luật nhảy từ 4 lên 6 không hoàn toàn tuyến tính. Tuy nhiên, so với các phương án khác, P có vẻ là lựa chọn có khả năng nhất nếu chấp nhận một quy luật hơi khác biệt. Hãy kiểm tra xem có quy luật nào khác dẫn đến E, G, hay H không. Nếu chữ còn thiếu là E (5), thì hiệu số là 2, 3, 4, -5. Không hợp lý. Nếu là G (7), hiệu số là 2, 3, 4, -3. Không hợp lý. Nếu là H (8), hiệu số là 2, 3, 4, -2. Không hợp lý. Do đó, với giả định rằng có một quy luật số học và phải chọn trong các đáp án, P với dãy hiệu 2, 3, 4, 6 là khả dĩ nhất.
Lời giải:
Đáp án đúng: A
Để giải bài toán này, chúng ta cần xác định giá trị cổ tức trên mỗi cổ phiếu. Gọi số cổ phiếu bà Long có năm ngoái là 'x' và giá trị cổ tức trên mỗi cổ phiếu là 'y' đô la.
Theo đề bài, năm ngoái bà Long nhận được 160 đô la tiền cổ tức, nên ta có phương trình: x * y = 160 (1).
Nếu bà Long có thêm 12 cổ phiếu, tức là bà có (x + 12) cổ phiếu, bà sẽ nhận được thêm 15 đô la tiền cổ tức. Điều này có nghĩa là tổng số cổ tức bà nhận được là 160 + 15 = 175 đô la. Ta có phương trình thứ hai: (x + 12) * y = 175 (2).
Bây giờ chúng ta sẽ giải hệ hai phương trình này. Từ phương trình (1), ta có y = 160/x. Thay biểu thức này vào phương trình (2):
(x + 12) * (160/x) = 175
160 + 1920/x = 175
1920/x = 175 - 160
1920/x = 15
x = 1920 / 15
x = 128
Vậy, năm ngoái bà Long đã có 128 cổ phiếu.
Kiểm tra lại:
Nếu x = 128, thì y = 160 / 128 = 1.25 đô la/cổ phiếu.
Nếu bà có thêm 12 cổ phiếu, tức là 128 + 12 = 140 cổ phiếu.
Tổng cổ tức bà nhận được là 140 * 1.25 = 175 đô la.
Số tiền cổ tức tăng thêm là 175 - 160 = 15 đô la. Điều này khớp với đề bài.
Theo đề bài, năm ngoái bà Long nhận được 160 đô la tiền cổ tức, nên ta có phương trình: x * y = 160 (1).
Nếu bà Long có thêm 12 cổ phiếu, tức là bà có (x + 12) cổ phiếu, bà sẽ nhận được thêm 15 đô la tiền cổ tức. Điều này có nghĩa là tổng số cổ tức bà nhận được là 160 + 15 = 175 đô la. Ta có phương trình thứ hai: (x + 12) * y = 175 (2).
Bây giờ chúng ta sẽ giải hệ hai phương trình này. Từ phương trình (1), ta có y = 160/x. Thay biểu thức này vào phương trình (2):
(x + 12) * (160/x) = 175
160 + 1920/x = 175
1920/x = 175 - 160
1920/x = 15
x = 1920 / 15
x = 128
Vậy, năm ngoái bà Long đã có 128 cổ phiếu.
Kiểm tra lại:
Nếu x = 128, thì y = 160 / 128 = 1.25 đô la/cổ phiếu.
Nếu bà có thêm 12 cổ phiếu, tức là 128 + 12 = 140 cổ phiếu.
Tổng cổ tức bà nhận được là 140 * 1.25 = 175 đô la.
Số tiền cổ tức tăng thêm là 175 - 160 = 15 đô la. Điều này khớp với đề bài.
Lời giải:
Đáp án đúng: C
Để giải bài toán này, chúng ta cần xác định tuổi hiện tại của Mario trước, sau đó tính tuổi của anh ấy cách đây x năm.
Bước 1: Tìm tuổi hiện tại của Mario.
Nếu 8 năm trước Mario 32 tuổi, thì tuổi hiện tại của anh ấy là 32 + 8 = 40 tuổi.
Bước 2: Tính tuổi của Mario cách đây x năm.
Tuổi của Mario cách đây x năm sẽ bằng tuổi hiện tại trừ đi x, tức là 40 - x.
So sánh với các phương án:
- Phương án A: x - 40 (Sai)
- Phương án B: x - 24 (Sai)
- Phương án C: 40 - x (Đúng)
- Phương án D: 24 - x (Sai)
Vậy, đáp án đúng là 40 - x.
Bước 1: Tìm tuổi hiện tại của Mario.
Nếu 8 năm trước Mario 32 tuổi, thì tuổi hiện tại của anh ấy là 32 + 8 = 40 tuổi.
Bước 2: Tính tuổi của Mario cách đây x năm.
Tuổi của Mario cách đây x năm sẽ bằng tuổi hiện tại trừ đi x, tức là 40 - x.
So sánh với các phương án:
- Phương án A: x - 40 (Sai)
- Phương án B: x - 24 (Sai)
- Phương án C: 40 - x (Đúng)
- Phương án D: 24 - x (Sai)
Vậy, đáp án đúng là 40 - x.
Lời giải:
Đáp án đúng: C
Bài toán kiểm tra khả năng áp dụng định lý Pytago trong hình học không gian. Gọi D là vị trí nhà Dan, K là vị trí nhà Karen, và Q là vị trí quán cafe. Theo đề bài, khoảng cách giữa Dan và Karen là 10 dặm (DK = 10). Quán cafe nằm ở hướng Bắc nhà Dan và hướng Đông nhà Karen. Điều này có nghĩa là nếu ta coi nhà Dan là gốc tọa độ (0,0), thì nhà Karen sẽ ở tọa độ (0, -10) hoặc (10, 0) hoặc (-10, 0) hoặc (0, 10). Tuy nhiên, cách diễn đạt "hướng Bắc nhà Dan" và "hướng Đông nhà Karen" gợi ý một hệ tọa độ vuông góc. Giả sử nhà Dan ở tọa độ (0,0). Quán cafe ở hướng Bắc nhà Dan, nên tọa độ quán Q có dạng (x, y) với y > 0. Nhà Karen ở hướng Đông nhà Dan, nên tọa độ nhà Karen K có dạng (x', 0) với x' > 0. Khoảng cách DK = 10. Tuy nhiên, cách diễn đạt "hướng Bắc nhà Dan" và "hướng Đông nhà Karen" kết hợp với việc gặp nhau tại quán cafe cho thấy có thể hiểu như sau: D và K tạo thành hai đỉnh của một tam giác vuông với quán cafe Q là đỉnh góc vuông. Nếu vậy, D và K nằm trên hai trục vuông góc với nhau tại Q. Tuy nhiên, đề bài lại cho khoảng cách giữa Dan và Karen là 10 dặm. Cách diễn đạt "hướng Bắc nhà Dan" và "hướng Đông nhà Karen" nên được hiểu là Dan và Karen ở hai vị trí có tọa độ mà khi nối với quán cafe sẽ tạo thành hai cạnh vuông góc. Xét trường hợp đơn giản: Dan ở A, Karen ở B, quán cafe ở C. C nằm về phía Bắc của A và phía Đông của B. Nếu A là (0,0), thì C là (x, y) với x>0, y>0. Nếu B nằm về phía Nam của C, thì B có tọa độ (x, y-h). Tuy nhiên, cách diễn đạt "hướng Bắc nhà Dan" và "hướng Đông nhà Karen" gợi ý rằng đường thẳng nối Dan với quán cafe và đường thẳng nối Karen với quán cafe là vuông góc. Tức là, tam giác DKQ là tam giác vuông tại Q. Gọi DQ = a và KQ = b. Ta có a là khoảng cách từ nhà Dan đến quán cafe, và b là khoảng cách từ nhà Karen đến quán cafe. Theo đề bài, quán cafe gần nhà Dan hơn nhà Karen 2 dặm, tức là a = b - 2. Khoảng cách giữa nhà Dan và nhà Karen là 10 dặm, tức là DK = 10. Áp dụng định lý Pytago cho tam giác vuông DKQ: DQ^2 + KQ^2 = DK^2. Thay a và b vào: a^2 + b^2 = 10^2. Ta có hệ phương trình: 1) a = b - 2 2) a^2 + b^2 = 100. Thay (1) vào (2): (b - 2)^2 + b^2 = 100. b^2 - 4b + 4 + b^2 = 100. 2b^2 - 4b - 96 = 0. Chia cả hai vế cho 2: b^2 - 2b - 48 = 0. Phân tích phương trình bậc hai: (b - 8)(b + 6) = 0. Vì b là khoảng cách nên b > 0. Do đó, b = 8. Khoảng cách từ nhà Karen đến quán cafe là 8 dặm. Kiểm tra lại: Nếu b = 8, thì a = b - 2 = 8 - 2 = 6. a^2 + b^2 = 6^2 + 8^2 = 36 + 64 = 100. DK = sqrt(100) = 10. Điều này khớp với đề bài. Vậy, từ nhà Karen tới quán cafe là 8 dặm.
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP
Lời giải:
Bạn cần đăng ký gói VIP để làm bài, xem đáp án và lời giải chi tiết không giới hạn. Nâng cấp VIP

CEO.29: Bộ Tài Liệu Hệ Thống Quản Trị Doanh Nghiệp
628 tài liệu440 lượt tải

CEO.28: Bộ 100+ Tài Liệu Hướng Dẫn Xây Dựng Hệ Thống Thang, Bảng Lương
109 tài liệu762 lượt tải

CEO.27: Bộ Tài Liệu Dành Cho StartUp - Quản Lý Doanh Nghiệp Thời Đại 4.0
272 tài liệu981 lượt tải

CEO.26: Bộ Tài Liệu Dành Cho StartUp - Khởi Nghiệp Thời Đại 4.0
289 tài liệu690 lượt tải

CEO.25: Bộ Tài Liệu Ứng Dụng Công Nghệ Thông Tin và Thương Mại Điện Tử Trong Kinh Doanh
240 tài liệu1031 lượt tải

CEO.24: Bộ 240+ Tài Liệu Quản Trị Rủi Ro Doanh Nghiệp
249 tài liệu581 lượt tải
ĐĂNG KÝ GÓI THI VIP
- Truy cập hơn 100K đề thi thử và chính thức các năm
- 2M câu hỏi theo các mức độ: Nhận biết – Thông hiểu – Vận dụng
- Học nhanh với 10K Flashcard Tiếng Anh theo bộ sách và chủ đề
- Đầy đủ: Mầm non – Phổ thông (K12) – Đại học – Người đi làm
- Tải toàn bộ tài liệu trên TaiLieu.VN
- Loại bỏ quảng cáo để tăng khả năng tập trung ôn luyện
- Tặng 15 ngày khi đăng ký gói 3 tháng, 30 ngày với gói 6 tháng và 60 ngày với gói 12 tháng.
77.000 đ/ tháng
.png)
.png)
.png)
.png)
.png)
.png)