Câu hỏi:
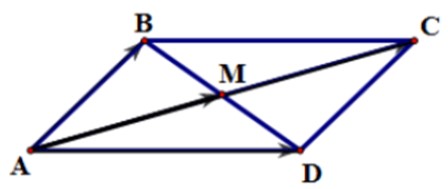
Cho hình bình hành ABCD. Hai điểm M, N lần lượt là trung điểm của BC và AD. Tìm đẳng thức sai?
Đáp án đúng: C
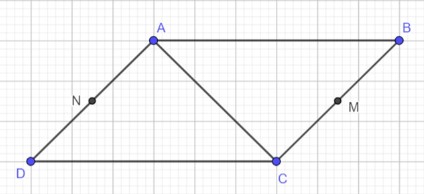
Ta xét từng đáp án:
Đáp án A: Theo quy tắc hình bình hành, ta có:
Tứ giác AMCN là hình bình hành ⇒ A đúng.
Đáp án B: Theo quy tắc hình bình hành, ta có:
Tứ giác ABCD là hình bình hành .
Mà từ đáp án A, ta có .
Do đó ta có ⇒ B đúng.
Đáp án C: Vì tứ giác AMCN là hình bình hành nên ta có và .
Do đó từ đáp án B, ta có ⇒ C đúng.
Đáp án D: Tứ giác ABCD là hình bình hành có AC và BD là hai đường chéo.
Do đó .
Vì vậy ⇒ D sai.
Đáp án đúng là: D
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Giữa Học Kì I - Toán 10 - (Năm 2023 - 2024) - Các Trường THPT Trên Toàn Quốc là tài liệu giúp học sinh hệ thống lại các kiến thức đã học thông qua các câu hỏi ngắn gọn và súc tích. Các bài tập được thiết kế phù hợp với nhiều đối tượng học sinh, từ cơ bản đến nâng cao.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026