Câu hỏi:
Cho đường tròn \((\mathrm{O} ; 8 \mathrm{~cm})\), cung nhỏ AB sao cho \(\widehat{\mathrm{AOB}}=90^{\circ}\)
Hình giới hạn bởi một cung nhỏ của một đường tròn và dây căng cung đó là hình viên phân.
Hình giới hạn bởi một cung nhỏ của một đường tròn và dây căng cung đó là hình vành khuyên.
Diện tích hình quạt tròn OAB là \(\mathrm{S} \approx 50,27\left(\mathrm{cm}^2\right)\) (kết quả làm tròn đến chữ số thập phân thứ hai).
Diện tích hình viên phân giới hạn bởi hình quạt tròn AOB và dây AB là \(28,27 \mathrm{~cm}^2\) (kết quả làm tròn đến chữ số thập phân thứ hai).
Đáp án đúng: Đúng, Sai, Đúng, Sai
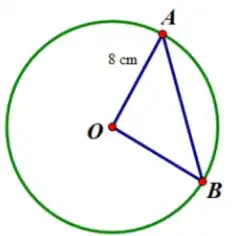
a) Hình giới hạn bởi một cung nhỏ của một đường tròn và dây căng cung đó là hình viên phân.
b) Sai.
c) \(\mathrm{S}=\frac{\pi \mathrm{R}^2 \mathrm{n}}{360}=\frac{\pi \cdot 8^2 \cdot 90}{360} \approx 50,27\left(\mathrm{cm}^2\right)\)
d) Ta có \(\triangle \mathrm{OAB}\) là tam giác vuông cân tại \(\mathrm{O}, \mathrm{OA}=\mathrm{OB}=8 \mathrm{cm}\)
\(\Rightarrow \mathrm{S}_{\mathrm{OAB}}=\frac{1}{2} \mathrm{OA} \cdot \mathrm{OB}=\frac{1}{2} \cdot 8 \cdot 8=32\left(\mathrm{cm}^2\right)\)
Diện tích hình viên phân giới hạn bởi hình quạt tròn OAB và dây AB là:
\(\mathrm{S}_{\mathrm{vp}}=\mathrm{S}_{\mathrm{q}}-\mathrm{S}_{\mathrm{OAB}}=50,27-32=18,27\left(\mathrm{cm}^2\right)\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Học Kì I – Toán 9 – Kết Nối Tri Thức Với Cuộc Sống – Bộ Đề 01 bao gồm hệ thống câu hỏi trắc nghiệm và tự luận bám sát nội dung chương trình Toán 9 học kì I, tập trung vào các chủ đề như căn bậc hai, hàm số bậc nhất, hệ phương trình và ứng dụng thực tế. Bộ đề giúp học sinh rèn luyện kỹ năng giải bài, củng cố kiến thức và chuẩn bị hiệu quả cho kì kiểm tra học kì I.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026