500 câu trắc nghiệm giữa HK1 Toán 9 - CTST - Đề 1

a) Thay \(x=5\) và \(y=-1\) vào phương trình đã cho, ta được:

\(5+2 \cdot(-1)=3 .\)

Suy ra cặp số \((5 ;-1)\) là một nghiệm của phương trình \(x+2 y=3\).

b) Phương trình \(x+2 y=3\) là phương trình bậc nhất hai ẩn. 

c) Viết lại phương trình \(x+2 y=3\) thành \(y=\frac{3}{2}-\frac{1}{2} x\), khi đó tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng \(y=\frac{3}{2}-\frac{1}{2} x\). 

d) Phương trình \(x+2 y=3\) là phương trình bậc nhất hai ẩn, có vô số nghiệm.

Viết lại phương trình \(x+2 y=3\) thành \(x=3-2 y\).

Khi đó, nghiệm tổng quát của phương trình đó là: \((3-2 y ; y)\) với \(y \in \mathbb{R}\) tùy ý. 

Để cặp số \((-2 ; 3)\) là nghiệm của hệ phương trình, ta thay \(x=-2\) và \(y=3\) vào hệ phương trình, ta được: \(\left\{\begin{array}{l}a .(-2)+3=5 \\ 3 .(-2)+b .3=0\end{array}\right.\)

Giải hệ phương trình trên, ta được: \(\left\{\begin{array}{l}-2 a=2 \\ -6+3 b=0\end{array}\right.\) hay \(\left\{\begin{array}{l}a=-1 \\ b=2 \end{array}\right.\)

Vậy, để cặp số \((-2 ; 3)\) là nghiệm của hệ phương trình thì \(a=-1\) và \(b=2\).

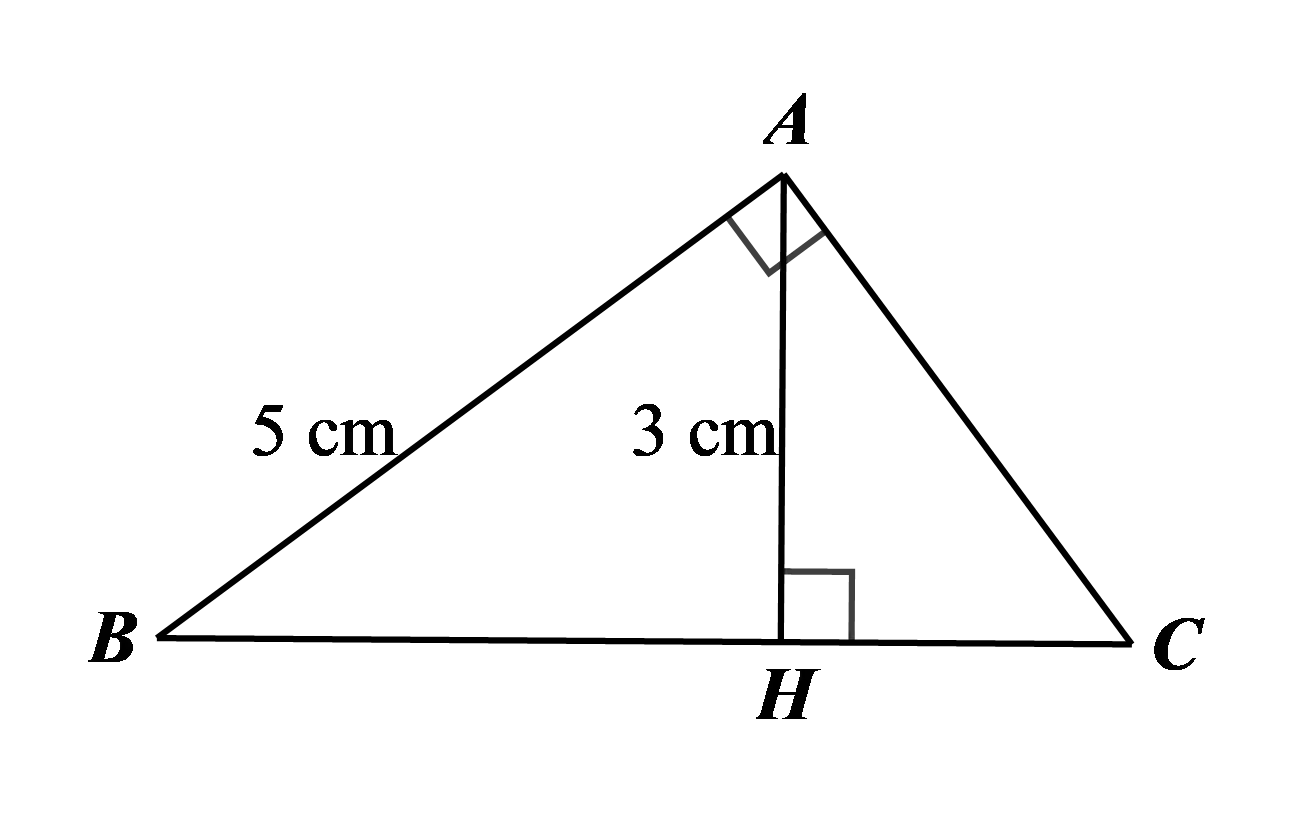
Xét \(\triangle A B H\) vuông tại \(H\), ta có: \(\sin B=\frac{A H}{A B}=\frac{3}{5}\).

Xét \(\triangle A B C\) vuông tại \(A\), ta có:

\(\widehat{B}+\widehat{C}=90^{\circ}, \text { suy ra } \cos C=\sin B=\frac{3}{5} .\)

Sử dụng MTCT, ta có kết quả \(53^{\circ} 7^{\prime} 48.37^{\prime \prime}\), làm tròn đến phút ta được \(53^{\circ}\).

Vì \(x + 2 \ne 0\) khi \(x \ne - 2\) và \(x - 1 \ne 0\) khi \(x \ne 1\) nên điều kiện xác định của phương trình \(\frac{1}{{x + 2}} + 1 = \frac{2}{{x - 1}}\) là \(x \ne - 2\) và \(x \ne 1\).

Ta có: \(\left( {\frac{2}{3}x + 6} \right)\left( {8 - 2x} \right) = 0\)

\(\frac{2}{3}x + 6 = 0\) hoặc \(8 - 2x = 0\)

\(\frac{2}{3}x = - 6\) hoặc \(2x = 8\)

\(x = - 9\) hoặc \(x = 4\)

Vậy phương trình đã cho có hai nghiệm là \(x = - 9\,;\) \(x = 4\).