Hạt pôlôni \(({}_{84}^{210}\text{Po})\) đang đứng yên thì phân rã alpha (α) và biến đổi thành hạt X được minh họa như hình bên. Lấy khối lượng các hạt nhân tính theo đơn vị amu gần bằng số khối của của chúng.
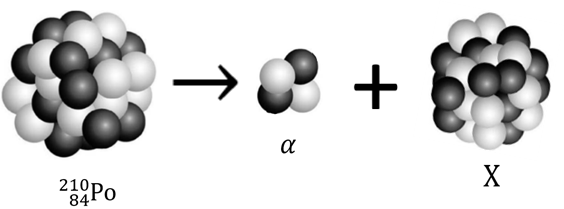
a) Số nuclon của hạt X là 206.
b) Hạt α và hạt X chuyển động ngược chiều nhau.
c) Tỉ số giữa tốc độ của hạt α và hạt X ngay sau phản ứng xảy ra là 52,5.
d) Động năng của hạt α bay ra chiếm khoảng 98,1% năng lượng tỏa ra của phản ứng.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
a) Đúng.
Phương trình phản ứng phân rã alpha \((\alpha ={}_{2}^{4}\text{He})\) của pôlôni \(({}_{84}^{210}\text{Po})\) là
\({}_{84}^{210}\text{Po}\to {}_{2}^{4}\text{He}+{}_{\text{Z}}^{\text{A}}\text{X}\).
Áp dụng định luật bảo toàn số nuclôn và định luật bảo toàn điện tích ta được

Hạt X là hạt chì, phương trình phản ứng phân rã alpha \((\alpha ={}_{2}^{4}\text{He})\) của pôlôni \(({}_{84}^{210}\text{Po})\) được viết tường minh là
\({}_{84}^{210}\text{Po}\to {}_{2}^{4}\text{He}+{}_{82}^{206}\text{Pb}\).
b) Đúng.
Ngay trước phân rã, động lượng của hệ là động lượng của hạt pôlôni và bằng không vì hạt pôlôni đứng yên. Ngay sau phân rã, vectơ động lượng của hệ là tổng vectơ động lượng của hạt alpha và hạt chì. Áp dụng định luật bảo toàn động lượng ta được
\({{\vec{p}}_{\text{ }\!\!\alpha\!\!\text{ }}}+{{\vec{p}}_{\text{Pb}}}=\vec{0}\leftrightarrow {{\vec{p}}_{\text{ }\!\!\alpha\!\!\text{ }}}=-{{\vec{p}}_{\text{Pb}}}\leftrightarrow {{m}_{\alpha }}{{\vec{v}}_{\text{ }\!\!\alpha\!\!\text{ }}}=-{{m}_{\text{Pb}}}{{\vec{v}}_{\text{Pb}}}\leftrightarrow {{\vec{v}}_{\text{ }\!\!\alpha\!\!\text{ }}}=-\dfrac{{{m}_{\text{Pb}}}}{{{m}_{\alpha }}}{{\vec{v}}_{\text{Pb}}}\).
Như vậy \({{\vec{v}}_{\text{ }\!\!\alpha\!\!\text{ }}}\) và \({{\vec{v}}_{\text{Pb}}}\) ngược chiều nhau, tức là hạt α và hạt chì chuyển động ngược chiều nhau.
c) Sai.
Từ biểu thức trên ta có
\(\dfrac{{{v}_{\text{ }\!\!\alpha\!\!\text{ }}}}{{{v}_{\text{Pb}}}}=\dfrac{{{m}_{\text{Pb}}}}{{{m}_{\alpha }}}=\dfrac{206}{4}=51,5\).
d) Đúng.
Từ biểu thức \({{\vec{p}}_{\text{ }\!\!\alpha\!\!\text{ }}}+{{\vec{p}}_{\text{Pb}}}=\vec{0}\) ta suy ra \({{\vec{p}}_{\text{ }\!\!\alpha\!\!\text{ }}}=-{{\vec{p}}_{\text{Pb}}}\), nghĩa là vectơ động lượng của hạt alpha và của hạt chì có chiều ngược nhau nhưng có độ lớn bằng nhau. Về độ lớn ta có
\({{p}_{\text{ }\!\!\alpha\!\!\text{ }}}={{p}_{\text{Pb}}}\).
Hạt có khối lượng m, có độ lớn vận tốc v thì độ lớn động lượng và động năng của hạt lần lượt là \(p=mv\) và \(K=\dfrac{1}{2}m{{v}^{2}}\). Từ đó ta có mối liên hệ giữa p, K và m là
\({{p}^{2}}=2mK\).
Do đó, từ \({{p}_{\text{ }\!\!\alpha\!\!\text{ }}}={{p}_{\text{Pb}}}\) hay \(p_{\text{ }\!\!\alpha\!\!\text{ }}^{2}=p_{\text{Pb}}^{2}\) và công thức liên hệ \({{p}^{2}}=2mK\) ta suy ra \(2{{m}_{\text{ }\!\!\alpha\!\!\text{ }}}{{K}_{\text{ }\!\!\alpha\!\!\text{ }}}=2{{m}_{\text{Pb}}}{{K}_{\text{Pb}}}\) hay là
\(\dfrac{{{K}_{\text{ }\!\!\alpha\!\!\text{ }}}}{{{K}_{\text{Pb}}}}=\dfrac{{{m}_{\text{Pb}}}}{{{m}_{\text{ }\!\!\alpha\!\!\text{ }}}}\).
Như vậy, động năng của hai hạt bay ra tỉ lệ nghịch với khối lượng của chúng.
Ngay trước phân rã thì hạt pôlôni đứng yên nên động năng của nó bằng không. Với chú ý đó, áp dụng định luật bảo toàn năng lượng ta được
\({{m}_{\text{Po}}}{{c}^{2}}={{m}_{\text{ }\!\!\alpha\!\!\text{ }}}{{c}^{2}}+{{K}_{\text{ }\!\!\alpha\!\!\text{ }}}+{{m}_{\text{Pb}}}{{c}^{2}}+{{K}_{\text{Pb}}}\).
Năng lượng phản ứng tỏa ra là \(W=\left[ {{m}_{\text{Po}}}-({{m}_{\text{ }\!\!\alpha\!\!\text{ }}}+{{m}_{\text{Pb}}}) \right]{{c}^{2}}\). Kết hợp với biểu thức mô tả sự bảo toàn năng lượng ở ngay trên ta được
\(W={{K}_{\text{ }\!\!\alpha\!\!\text{ }}}+{{K}_{\text{Pb}}}\).
Từ biểu thức \(\dfrac{{{K}_{\text{ }\!\!\alpha\!\!\text{ }}}}{{{K}_{\text{Pb}}}}=\dfrac{{{m}_{\text{Pb}}}}{{{m}_{\text{ }\!\!\alpha\!\!\text{ }}}}\) và biểu thức \(W={{K}_{\text{ }\!\!\alpha\!\!\text{ }}}+{{K}_{\text{Pb}}}\) ở ngay trên ta suy ra
\({{K}_{\text{ }\!\!\alpha\!\!\text{ }}}=\dfrac{{{m}_{\text{Pb}}}}{{{m}_{\text{ }\!\!\alpha\!\!\text{ }}}+{{m}_{\text{Pb}}}}W\).
Thay mPb ≈ 206u và mα ≈ 4u vào biểu thức ngay trên ta tính được
\({{K}_{\text{ }\!\!\alpha\!\!\text{ }}}\approx 98,1%W\).
Như vậy, động năng của hạt alpha bay ra chiếm khoảng 98,1% năng lượng tỏa ra của phản ứng.
Tuyển Tập Đề Thi Tham Khảo Tốt Nghiệp THPT Năm 2025 - Vật Lí - Bộ Đề 07 là tài liệu ôn tập quan trọng dành cho học sinh lớp 12, giúp các em rèn luyện kỹ năng làm bài và chuẩn bị tốt nhất cho kỳ thi tốt nghiệp THPT 2025. Bộ đề được biên soạn theo định hướng của Bộ GD ĐT, bám sát chương trình học, bao gồm các chủ đề quan trọng như cơ học, điện học, quang học, dao động và sóng, vật lý hạt nhân… Hệ thống câu hỏi trắc nghiệm phong phú, được thiết kế theo nhiều mức độ từ nhận biết, thông hiểu đến vận dụng và vận dụng cao, giúp học sinh làm quen với cấu trúc đề thi và phát triển kỹ năng phân tích, tư duy logic. Mỗi đề thi đều có đáp án chi tiết và hướng dẫn giải cụ thể, hỗ trợ học sinh tự đánh giá năng lực, xác định điểm mạnh và cải thiện điểm yếu trong quá trình ôn tập.
Câu hỏi liên quan
Khối lượng của các hạt proton, neutron và hạt nhân \(_{8}^{18}O\) lần lượt là 1,0073 amu; 1,0087 amu; 17,9948 amu. Biết 1 amu = 931,5 MeV/c2.
Năng lượng liên kết của hạt nhân \(_{8}^{18}O\) là bao nhiêu MeV (làm tròn kết quả đến chữ số hàng đơn vị)?
Trong hạt nhân của một nguyên tử có 8 proton và 9 neutron. Năng lượng liên kết riêng của hạt nhân này bằng \(7,75 \mathrm{MeV} /\) nucleon. Biết \(\mathrm{m}_{\mathrm{p}}=1,0073 \mathrm{amu}, \mathrm{m}_{\mathrm{n}}=1,0087 \mathrm{amu}\) và \(1 \mathrm{amu} \approx 931,5 \mathrm{MeV} / \mathrm{c}^{2}\).
Khối lượng của hạt nhân đó bằng:
Với c là tốc độ ánh sáng trong chân không, \(\mathrm{m}_{0}\) là khối lượng nghỉ của hạt. Khi hạt chuyển động với tốc độ \(\mathrm{v}(\mathrm{v}<\mathrm{c})\) thì năng lượng toàn phần E của hạt được tính theo công thức
Một hạt nhân có độ hụt khối càng lớn thì hạt nhân đó
Biết khối lượng của các hạt nhân Cacbon mC = 12,000 amu, mα= 4,0015 amu, mp= 1,0073 amu, mn= 1,0087 amu và 1 amu = 931 MeV/c². Năng lượng cần thiết tối thiểu để chia hạt nhân \(_{6}^{12}C\)thành ba hạt α theo đơn vị Jun là X.10-13 J. Tìm X (Kết quả làm tròn đến chữ số thứ nhất sau dấu phẩy)
Giả sử có một lượng hạt nhân \({}_{92}^{235}\text{U}\) đủ nhiều và ban đầu ta kích thích cho \({{N}_{0}}={{10}^{10}}\) hạt nhân \({}_{92}^{235}\text{U}\) phân hạch. Gọi \(k\) là số neutron trung bình được giải phóng sau mỗi phân hạch đến kích thích các hạt nhân \({}_{92}^{235}\text{U}\) khác để tạo nên những phản ứng phân hạch mới, hình thành dây chuyền phản ứng. Mỗi hạt nhân \({}_{92}^{235}\text{U}\) phân hạch tỏa ra năng lượng \({{E}_{1}}=200~\text{MeV}\). Năng lượng toả ra sau 10 phân hạch dây chuyền đầu tiên (kể cả phân hạch kích thích ban đầu) là \(E=708~\text{J}\). Lấy \(1~\text{eV}=1,{{6.10}^{-19}}~\text{J}\). Giá trị của \(k\) là bao nhiêu (làm tròn kết quả đến chữ số hàng phần mười)?
Biết khối lượng của proton là 1,00728 amu; của neutron là 1,00866 amu; của hạt nhân \({}_{11}^{23}\text{Na}\) là 22,98373 amu và 1 amu = 931,5 MeV/c2. Năng lượng liên kết của \({}_{11}^{23}\text{Na}\) bằng bao nhiêu MeV (làm tròn kết quả đến hàng đơn vị) ?
Phát biểu nào sau đây về phản ứng nhiệt hạch là đúng?
Hạt nhân càng bền vững nếu nó có...
Các phản ứng hạt nhân không tuân theo
Đại lượng đặc trưng cho mức độ bền vững của hạt nhân là
Cho phản ứng hạt nhân: \(_{11}^{23}Cl+_{1}^{2}D\to _{2}^{4}He+_{10}^{20}Ne\). Biết \({{m}_{Na}}=22,9327u\); \({{m}_{He}}=4,0015u\); \({{m}_{Ne}}=19,9870u\). ; \({{m}_{D}}=1,0073u\). Phản ứng trên tỏa hay thu một năng lượng bằng bao nhiêu?
Cho khối lượng nguyên tử của đồng vị cacbon \({}_{6}^{13}C\); êlectron; proton và neutron lần lượt là 12112,490 MeV/c2 ; 0,511 MeV/c2 ; 938,256 MeV/c2 và 939,550 MeV/c2. Năng lượng liên kết của hạt nhân \({}_{6}^{13}C\) bằng bao nhiêu MeV? (Kết quả làm tròn đến hàng đơn vị).
Xét phản ứng tổng hợp hạt nhân: \(_{1}^{2}D+_{1}^{2}D\to _{2}^{3}He+_{0}^{1}n\). Biết rằng, khối lượng của các nguyên tử \(_{1}^{2}D\), \(_{2}^{4}He\) và khối lượng hạt neutron lần lượt là 2,0141u; 3,0160u; 1,0087u.
Biết rằng mỗi hạt nhân \(_{92}^{235}U\) phân hạch tỏa ra trung bình 200,0 MeV. Năng lượng tỏa ra khi tổng hợp hoàn toàn 1,00 g deterium theo phản ứng trên tương đương với năng lượng tỏa ra khi bao nhiêu gam \(_{92}^{235}U\) phân hạch hoàn toàn (làm tròn kết quả đến chữ số hàng phần trăm)?
Cho các hạt nhân sau \({}_{92}^{238}\text{U}\), \({}_{92}^{235}\text{U}\), \({}_{11}^{23}\text{Na}\), \({}_{79}^{197}\text{Au}\). Biết rằng khối lượng của các hạt nhân \({}_{92}^{238}\text{U}\), \({}_{92}^{235}\text{U}\), \({}_{11}^{23}\text{Na}\), \({}_{79}^{197}\text{Au}\) và khối lượng của proton, neutron lần lượt là \({{\text{m}}_{\text{U}238}}\) = 238,050788 amu; \({{\text{m}}_{\text{U}235}}\) = 234,993422 amu, \({{\text{m}}_{\text{Na}23}}\) = 22,983730 amu, \({{\text{m}}_{\text{Au}197}}\) = 196,966552 amu, mp = 1,007276 amu và mn = 1,008665 amu. Lấy \(1\text{ }\!\!~\!\!\text{ u}{{\text{c}}^{2}}=931,5\text{ }\!\!~\!\!\text{ MeV}\). Thứ tự sắp xếp các hạt nhân nói trên theo mức độ bền vững tăng dần là
Cho khối lượng của proton, neutron và khối lượng của hạt nhân \({}_{18}^{40}\text{Ar}\), \({}_{3}^{6}\text{Li}\) lần lượt là 1,0073 amu, 1,0087 amu và 39,9525 amu, 6,0145 amu. Lấy 1 amu = 931,5 MeV/c2. Năng lượng liên kết riêng của hạt nhân \({}_{18}^{40}\text{Ar}\) gấp x lần năng lượng liên kết riêng của hạt nhân \({}_{3}^{6}\text{Li}\). Giá trị của x là bao nhiêu (làm tròn kết quả đến chữ số hàng phần trăm)?
Trong các phản ứng hạt nhân tỏa năng lượng. Nhận định nào sau đây không chính xác?
Hạt nhân càng bền vững nếu nó có
Cho phản ứng tổng hợp hạt nhân:
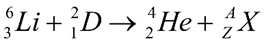
Biết khối lượng nguyên tử của các hạt là mD = 2,01410 u; mLi = 6,01512 u; mHe = 4,00260 u. Tính năng lượng toả ra của phản ứng. (Viết kết quả theo đơn vị MeV và lấy đến một chữ số sau dấu phẩy thập phân).
Trong chuỗi phản ứng prton-proton trong lòng Mặt Trời có hai phản ứng riêng biệt trong đó 4 hạt nhân hydro cuối cùng có thể dẫn đến 1 hạt nhân Heli. Trong chuỗi phản ứng này, phản ứng \(_{1}^{2}D+_{1}^{1}H\to _{2}^{3}He+\gamma\) tạo ra bức xạ điện từ gamma. Biết \({{m}_{p}}=1,00728\left( u \right)\); \({{m}_{D}}=2,0135\left( u \right)\); \({{m}_{He}}=3,0149\left( u \right) \). Lấy 1u = 931,5 MeV/c2. Giả sử hạt nhân Heli sinh ra trong lõi Mặt Trời chuyển động nhiệt ở nhiệt độ trung bình vào khoảng 13,6.106 (°C) (nhiệt độ trong lòng Mặt Trời ). Động năng trung bình của chuyển động nhiệt của khí \(_{2}^{3}He\) chiếm xấp xỉ bao nhiêu phần trăm so với năng lượng phản ứng tỏa ra? (Coi các hạt nhân \(_{2}^{3}He\) là các phân tử khí lí tưởng)















