Địa hình của Cộng hòa Nam Phi chủ yếu là gì?

Đâu là thế mạnh nổi bật ở phần lãnh thổ phía tây Liên bang Nga?

Đọc bài thơ sau đây và trả lời câu hỏi:

Bất chợt đêm trăng mất điện

Vóng lên tiếng kêu hoài nhớ ngọn đèn dầu

Người xa xứ hỏi con đường cũ:

"Làng ta đang ở đâu"

Làng ta đang ở đâu!

Đêm Trung thu nào thấy bóng đa

Mái đình trùng tu đổi màu rêu cũ

Mẹ về chợ, mớ rau trong rổ nhựa

Bà lên chùa, phẩm oản gói ni lông

Vịt siêu trứng không mò cua bắt ốc

Gà gia công không nhặt thóc đống rơm

Con ếch, con lươn lên hàng đặc sản

Con cà cuống cay nơi khách sạn thị thành.

Làng tôi năm hai nghìn

Bao dập dồn hiện đại

Những đám rước bóng điện mờ điện nhạt

Những đám tang không chống gậy giật lùi

Bao ngỡ ngàng xuôi ngược

Tuổi mẫu giáo thi nhau làm sinh nhật

Tuổi cổ lai hy xây một trước cho mình

Bao đổi thay kỳ dị

Cô thợ cấy đấu cờ trên màn hình điện tử

Bác thợ cày hút thuốc lào mê bản tin quốc tế

Cả làng sôi lên cùng trái bóng châu Âu.

Làng tôi đang về đâu

Quê hương xưa hàng ngày thành khách lạ

Dân làng xưa không còn là người cũ

Bờ tre đổi hình

Ao làng đổi bóng

Nỗi nhớ  xa quê cũng thay đổi bóng hình.

Làng tôi năm hai nghìn

Người về quê cầm tiếng ô tô tìm chùm khế ngọt

Lạc vào vườn nhãn năm hoa

Lạc vào vườn hồng không hạt

Đêm hai nghìn sáng bừng nước mắt

Giọt lệ lăn về đâu!

(Rút trong tập thơ "Hạt gạo đồng trời" của Nguyễn Tấn Việt)

Đoạn thơ thứ ba thể hiện nội dung gì? 

Trồng dưa chuột áp dụng cho loại mô hình nào sau đây?

Nội dung nào sau đây phản ánh đúng ý nghĩa của Hiến chương ASEAN (2007) đối với sự phát triển của Hiệp hội các quốc gia Đông Nam Á?

Quả cầu nhỏ mang điện tích 10^-9 C đặt trong không khí. Cường độ điện trường tại 1 điểm cách quả cầu 5 cm là

Vì sao phương thức chăn thả tự do vẫn còn khá phổ biến ở các vùng nông thôn ở nước ta?

Bước 3 của quy trình vẽ hình chiếu trục đo là gì?

Cho hàm số bậc bốn \(f(x)\). Đồ thị hàm số \(y={{f}^{\prime }}(x)\) như hình vẽ.

Hàm số \(g(x)=f(x)+4x\) đồng biến trên khoảng nào?

Read the following passage about studying abroad and mark the letter A, B, C or D on your answer sheet to indicate the best answer to each of the following questions from 31 to 40.

Successful students often do the followings while studying. First, they have an overview before reading. Next, they look for important information and pay greater attention to it (which often needs jumping forward or backward to process information). They also relate important points to one another. Also, they activate and use their prior knowledge. When they realize that their understanding is not good, they do not wait to change strategies. Last, they can monitor understanding and take action to correct or “fix up” mistakes in comprehension.

Conversely, students with low academic achievement often demonstrate ineffective study skills. [I] They tend to assume a passive role in learning and rely on others (e.g., teachers, parents) to monitor their studying. [II] For example, low-achieving students often do not monitor their understanding of content; they may not be aware of the purpose of studying; and they show little evidence of looking back or employing “fix-up” strategies to fix understanding problems. [III] Students who struggle with learning new information seem to be unaware that they must extend effort beyond simply reading the content to understand and remember it. [IV] 

Children with learning disabilities do not plan and judge the quality of their studying. Their studying may be disorganized. Students with learning problems face challenges with personal organization as well. They often have difficulty keeping track of materials and assignments, following directions, and completing work on time. Unlike good studiers who employ a variety of study skills in a flexible yet purposeful manner, low-achieving students use a restricted range of study skills. They cannot explain why good study strategies are important for learning; and they tend to use the same, often ineffective study approach for all learning tasks, ignoring task content, structure or difficulty.

The phrase fix-up in paragraph 2 could be best replaced by_________. . 

Mối quan hữu cơ giữa các cấp độ tổ chức dựa trên

Bạn A thả quả bóng cao su từ độ cao \(10\) m theo phương thẳng đứng. Mỗi khi chạm đất nó lại nảy lên theo phương thẳng đứng có độ cao bằng \(\frac{3}{4}\) độ cao trước đó. Tính tổng quãng đường bóng đi được đến khi bóng dừng hẳn (đơn vị mét).

Trong hình ảnh sau đây, bộ máy Golgi nằm ở vị trí số mấy?

Find the mistake: She has disappeared four days ago, and they are still looking for her now.

Cho hàm số \(y=f\left( x \right)\) xác định trên đoạn \(\left[ -3;2 \right]\) và có đồ thị như hình vẽ sau.

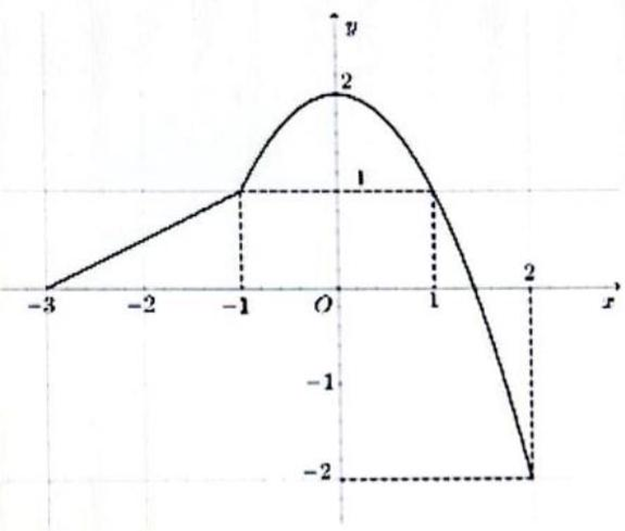
Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=f\left( x \right)\) trên đoạn \(\left[ -3;2 \right]\). Khi đó, giá trị \(M-2m\) bằng:

Read the following passage about The Longitude Prize and mark the letter A, B, C, or D on your answer sheet to indicate the best answer to each of the following questions

     On a stormy night in 1707, four ships struck rocks off the south coast of England and sank. [I] One thousand, four hundred sailors were drowned. [II] The ships had crashed because they had no way of knowing how far they had travelled in a particular direction; they could not calculate their longitude, which required accurate time measurement. [III] In such difficult circumstances, they believed that the best response to the disaster was a competition: the Longitude Prize. [IV]

     The Longitude Prize was no ordinary competition. To win it, someone had to find a way of calculating how far a ship had travelled east or west from its point of departure. Geniuses such as Sir Isaac Newton had failed to find a solution, so to ensure the interest of Britain’s greatest scientific minds, the government offered a prize of £20,000 — the equivalent of £2.6 million in today’s money. But to everyone’s surprise, it wasn’t a famous academic who solved the problem, but an unknown carpenter.

     When John Harrison wasn’t working with wood, he was making clocks. An accurate clock would allow sailors to calculate their position, but at the time it was thought impossible to create a mechanical clock that could work on a ship. The movement of the sea and the changes in temperature destroyed the delicate parts. However, after three frustrated attempts, Harrison’s fourth sea clock, H4, finally triumphed. Its mechanics were so good that the H4 worked better than most clocks on land.

   The Longitude Prize and Harrison’s success generated a lot of interest in the 18th century, but it was soon forgotten. However, in 2013, the British government created a new Longitude Prize, offering £10 million to the person who could solve a great challenge to humanity. An enthralled public then took part in a TV programme where viewers chose one challenge from a list of six for scientists to focus on. The question now is, will someone be able to solve it just as well as Harrison solved the challenge presented to him?

According to paragraph 4, which of the following is NOT a problem that arose from using mechanical clocks on ships?

Which of the following best restates each of the given sentences?

Nobody saw Peter at the year-end party of our company last night.

Read the following passage about the Second Acts That Inspire and mark the letter A, B, C or D on your answer sheet to indicate the best answer to each of the following questions from 31 to 40.

Life often presents us with unexpected challenges that force us back to the drawing board. Whether due to personal setbacks, career changes, or unforeseen circumstances, the courage to begin again can lead to remarkable transformations. Many inspiring individuals have shown that it's never too late to reinvent oneself and pursue new dreams. Throughout history, countless people have overcome seemingly impossible situations through sheer determination.

[I] Take J.K. Rowling, for instance. Before becoming a literary sensation, she was a struggling single mother living on welfare. [II] Her determination eventually paid off when her books became a global phenomenon, proving that setbacks can become stepping stones to success. [III] This remarkable turnaround demonstrates how resilience and unwavering belief in oneself can overcome seemingly insurmountable obstacles. Despite facing depression and financial hardship, she never gave up on her dreams. [IV]

Colonel Harland Sanders' story is another testament to the power of starting anew. At the age of 65, when most people contemplate retirement, he found himself struggling financially after his restaurant failed. Instead of giving up, he traveled across America, sleeping in his car while pitching his chicken recipe to restaurant owners. His recipe for success wasn't just about the perfect blend of herbs and spices; it was about persistence and determination. After facing over 1,000 rejections, he finally established Kentucky Fried Chicken, which grew into a global empire. His unwavering spirit and dedication inspired generations of entrepreneurs worldwide.

These inspiring stories remind us that failure is not final, but rather a chance to redirect our path. Every setback carries the seed of an equal or greater opportunity, and sometimes the end of one chapter is simply the beginning of a better one. The key lies in having the courage to take that first step, even when the future seems uncertain. As these remarkable individuals have shown, it's never too late to rewrite your story and create a powerful second act. Their journeys teach us that persistence and courage ultimately lead to success.

Based on the passage, which of the following is NOT MENTIONED?

Mark the letter A, B, C, or D on your answer sheet to indicate the correct answer to each of the following questions.

The chief foods eaten in any country depend largely on________ best in its climate and soil.

Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ sau:

Phương trình \(f\text{ }\!\!'\!\!\text{ }\left[ 5-3f\left( x \right) \right]=0\) có bao nhiêu nghiệm thực?