Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10;3;0) và chuyển động đều theo đường cáp có vecto chỉ phương là \(\vec{u} = (2;-2;1)\) với tốc độ là 4,5 m/s (đơn vị trên mỗi trục tọa độ là mét). Sau thời gian 180 giây, cabin dừng ở điểm B. Tìm tung độ điểm B.

Trong không gian với hệ tọa độ \(Oxyz\), góc tạo bởi hai vectơ \(\overrightarrow{a}=(-4;2;4)\) và \(\overrightarrow{b}=(2\sqrt{2};-2\sqrt{2};0)\) là:

Một tháp kiểm soát không lưu ở sân bay cao 109 m đặt một đài kiểm soát không lưu ở độ cao 105 m. Máy bay trong phạm vi cách dài kiểm soát 450 km sẽ hiển thị trên màn hình ra đa. Chọn hệ trục toạ độ \(Oxyz\) có gốc \(O\) trùng với vị tri chân tháp, mặt phẳng (\(Ox{y}'\)) trùng với mặt đất sao cho trục \(Ox\) là hướng Tây, trục \(Oy\) là hướng Nam và trục \(Oz\) là trục thẳng đứng (Hình vẽ), đơn vị trên mỗi trục là kilômét. Một máy bay đang ở vị trí \(A\) cách mặt đất 8 km, cách 268 km về phía Đông, 185 km về phía Nam so với tháp kiểm soát không lưu và đang chuyển động theo đường thẳng \(d\) có vectơ chỉ phương là \(\overrightarrow{u}=\left( 82;76;0 \right)\) hướng về đài kiểm soát không lưu.

Khi gắn hệ tọa độ \(O x y\) (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng \((O x y)\) trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí \(A(3 ;-2 ; 3)\) đến vị trí \(B(8 ; 8 ; 0)\). Góc giữa đường bay (một phần của đường thẳng \(A B\) và sân bay (một phần của mặt phẳng \((O x y)\)) bằng \(\alpha\) độ. Khi đó, giá trị của \(\alpha\) bằng bao nhiêu (làm tròn kết quả đến hàng đơn vị)?

Trong không gian \(Oxyz\), cho hai điểm \(A\left( 5;0;6 \right)\) và \(B\left( 3;5;0 \right)\). Điểm \(M\) di động trên trục \(Oz\), điểm \(N\) di động trên trục \(Oy\). Độ dài đường gấp khúc \(AMNB\) có độ dài nhỏ nhất bằng bao nhiêu? (kết quả làm tròn đến hàng phần mười).

Trong không gian với hệ tọa độ \(Oxyz\), cho điểm \(M\left( 1;2;3 \right)\). Gọi \({{M}_{1}},{{M}_{2}}\) lần lượt là hình chiếu vuông góc của \(M\) lên các trục \(Ox,Oy\). Vectơ nào dưới đây là một véctơ chỉ phương của đường thẳng \({{M}_{1}}{{M}_{2}}\)?

Trong không gian với một hệ trục tọa độ cho trước (đơn vị tính bằng mét), một con chim đang bay với tốc độ và hướng không đổi từ điểm \(A(20;40;30)\) đến điểm \(B(40;50;50)\) trong vòng \(4\) phút. Nếu con chim bay tiếp tục giữ nguyên vận tốc và hướng bay thì sau \(2\) phút con chim ở vị trí \(C(a;b;c)\). Tổng \(a+b+c\) bằng bao nhiêu?

Trong không gian \(\text{Ox}yz\), cho hình lập phương \(ABCD.A'B'C'D'\) có \(A\left( 0;0;0 \right)\), \(B\left( 2;0;0 \right)\), \(D\left( 0;2;0 \right)\), \(A'\left( 0;0;2 \right)\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AA'\) (Hình 3).

Trong không gian với hệ trục tọa độ \(Oxyz\), cho \(4\) điểm \(A\left( 2;4;-1 \right)\), \(B\left( 1;4;-1 \right)\), \(C\left( 2;4;3 \right)\), \(D\left( 2;2;-1 \right)\), biết \(M\left( x;y;z \right)\) để \(M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}+M{{D}^{2}}\) đạt giá trị nhỏ nhất thì \(x+y+z\) bằng bao nhiêu? (Lấy giá trị gần đúng làm tròn đến chữ số thập phân thứ hai)

Khi gắn hệ tọa độ \(Oxyz\) (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng \((Oxy)\) trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí \(A(5;~0;~5)\) đến vị trí \(B(10;~10;~3)\) và hạ cánh tại vị trí \(M(a;~b;~0).\) Giá trị của \(a+b\) bằng bao nhiêu ?

(Viết kết quả dưới dạng số thập phân)

Trong không gian với hệ tọa độ \(Oxyz\), một cabin cáp treo xuất phát tử điểm \(A\left( 1,2,3 \right)\) và chuyển động đều theo đường cáp có véc tơ chỉ phương \(\vec{u}=\left( 3,-4,2 \right)\) với tốc độ \(5\text{ }\!\!~\!\!\text{ m}/\text{s}\).

Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra không có đánh số \(\frac{7}{16}\). Hình minh hoạ sơ đồ một ngôi nhà trong hệ trục tọa độ \(Oxyz\), trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.

Trong không gian với hệ trục tọa độ \(Oxyz\), cho \(\vec{a}=\left( 2;-3;3 \right)\), \(\vec{b}=\left( 0;2;-1 \right)\), \(\vec{c}=\left( 3;-1;5 \right)\). Tọa độ của vecto \(\vec{u}=2\vec{a}+3\vec{b}-2\vec{c}\) là:

Trong không gian với hệ tọa độ Oxyz, một chiếc máy bay cất cánh từ điểm \(P(15;-4;2)\) và bay đều theo hướng của vecto \(\vec{d}=(3;1;-2)\) với tốc độ 5 m/s. Sau thời gian 200 giây, máy bay đến điểm Q. Tìm tung độ điểm Q (kết quả làm tròn đến hàng đơn vị).

Một nắp bể nước hình chữ nhật ABCD nằm cạnh bờ tường có kích thước \(9\text{dm}\times 12\text{dm}\) được kéo ra từ mặt sàn, do tác dụng của trọng lực nên nắp bề không thể mở ra được nếu không có người giữ. Người ta dùng một sợi dây xích dài 15 dm và kéo căng nối đỉnh \(C\) của hình chữ nhật với điểm \(M\) nằm phía trên bờ tường sao cho \(AM=9\text{dm}\) và AM vuông góc với mặt sàn. Chọn hệ trục \(Oxyz\) như hình vẽ, khi đó nắp bể mở ra và tạo với mặt sàn một góc \(\alpha \) (đơn vị trên mỗi trục tọa độ tính bằng dm). Bỏ qua độ dày của nắp bể.

Hai chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Bắc \(20\left( km \right)\) và về phía Tây \(10\left( km \right)\), đồng thời cách mặt đất \(0,7\left( km \right)\). Chiếc máy bay thứ hai cách điểm xuất phát về phía Đông \(30\left( km \right)\) và về phía Nam \(25\left( km \right)\), đồng thời cách mặt đất \(1\left( km \right)\). Hỏi hai chiếc máy bay cách nhau bao nhiêu \(km\)? (Làm tròn kết quả đến hàng đơn vị).

Trong không gian \(Oxyz\), một cabin cáp treo ở Bà Nà Hill xuất phát từ điểm \(A\left( -2;1;5 \right)\) và chuyển động đều theo đường cáp có vectơ chỉ phương là \(\vec{u}=\left( 0;-2;6 \right)\) với tốc độ là \(4\) m/s (đơn vị trên mỗi trục toạ độ là mét). Giả sử sau \(5\) (s) kể từ lúc xuất phát , cabin đến điểm \(M\). Gọi tọa độ \(M\left( a;b;c \right)\). Tính \(a+3b+c\).

Trên một phần mềm đã thiết kế sân khấu \(3\text{D}\) trong không gian \(Oxyz\). Tính \(cosin\) giữa hai tia sáng có phương trình lần lượt là \({{d}_{1}}:\frac{x}{2}=\frac{y}{1}=\frac{z}{-1},\) \({{d}_{2}}:\frac{x-1}{3}=\frac{y-1}{3}=\frac{z-1}{9}.\)

Một mái nhà hình tròn được đặt trên ba cây cột trụ. Các cây cột trụ vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 8m, 9m, 10m. Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 8 m. Chọn hệ trục tọa độ như hình vẽ, với \(B\) thuộc tia \(Ox,C\) thuộc tia \(Oy\), tia Oz cùng hướng với vectơ \(\overline{A{A}'}\); gốc toạ độ O trùng với trung điểm của \(AC\) và mỗi đơn vị trên trục có độ dài 1 mét (xem hình vẽ).

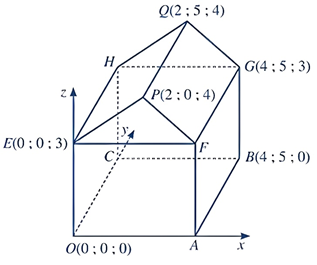
Một kho chứa hàng có dạng hình hộp chữ nhật \(ABCD.EFGH\) và mái che có dạng lăng trụ đứng \(EFP.HGQ\) với đáy \(\Delta EFP\) là tam giác cân đỉnh \(P\) và các điểm \(A;B;E;F;P\) cùng nằm trong một mặt phẳng. Gọi \(T\) là trung điểm của \(DC\). Các kích thước của kho chứa lần lượt là \(AB=6m\);\(AE=5m\); \(AD=8m\); \(QT=7m\). Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ có gốc toạ độ là điểm \(O\) thuộc đoạn \(AD\) sao cho \(OA=2m\) và các trục toạ độ tương ứng như hình vẽ dưới đây. Khi đó:

Trong không gian với hệ tọa độ \(Oxyz,\) đài kiểm soát không lưu sân bay có tọa độ \(O\left( 0;0;0 \right)\), mỗi đơn vị trên một trục ứng với \(1\text{ km}\). Máy bay bay trong phạm vi cách đài kiểm soát \(417\text{ km}\) sẽ hiển thị trên màn hình ra đMột máy bay đang ở vị trí \(A\left( -688;-185;8 \right)\), chuyển động theo đường thẳng \(d\) có vectơ chỉ phương là \(\overrightarrow{u}=\left( 91;75;0 \right)\) và theo hướng về đài không lưu. \(E\left( a;b;c \right)\) là vị trí sớm nhất mà máy bay xuất hiện trên màn hình. Tính \(T=a+b+c\).