Cho hàm số bậc ba có bảng biến thiên như hình vẽ dưới đây. Giá trị cực tiểu của hàm số là:

a) Đúng.

Ta có : \(f\left( x \right)=\sin x-x\)\(\Rightarrow {f}'\left( x \right)=\cos x-1\).

b) Sai.

Ta có: \({f}'\left( x \right)=\cos x-1\) khi đó:

\({f}'\left( x \right)=0\)\(\Leftrightarrow \cos x-1=0\)\(\Leftrightarrow \cos x=1\)\(\Leftrightarrow x=k2\pi \)\(\left( k\in \mathbb{Z} \right)\).

Do \(x\in \left[ \frac{\pi }{2};\frac{3\pi }{2} \right]\) nên \(\frac{\pi }{2}\le k2\pi \le \frac{3\pi }{2},k\in \mathbb{Z}\Leftrightarrow \frac{1}{4}\le k\le \frac{3}{4},k\in \mathbb{Z}\).

Suy ra phương trinh \({f}'\left( x \right)=0\) không có nghiệm trên đoạn \(\left[ \frac{\pi }{2};\frac{3\pi }{2} \right]\).

c) Đúng.

Do \({f}'\left( x \right)=\cos x-1<0,\forall x\in \left[ \frac{\pi }{2};\frac{3\pi }{2} \right]\) nên hàm số đã cho nghịch biến trên đoạn \(\left[ \frac{\pi }{2};\frac{3\pi }{2} \right]\).

Khi đó hàm số đạt GTNN là \(-1-\frac{3\pi }{2}\) tại \(x=\frac{3\pi }{2}\).

d) Đúng.

Do\(f\left( x \right)=\sin x-x\) nên ta có:

\(f\left( 0 \right)=\sin \left( 0 \right)-0=0\) và \(f\left( \pi  \right)=\sin \left( \pi  \right)-\pi =-\pi \).

a) Đúng.

Đường cáp đi qua điểm \(A\left( 10;3;0 \right)\) và có véctơ chỉ phương là \(\vec{u}=\left( 2;-2;1 \right)\) nên có phương trình chính tắc là \(\frac{x-10}{2}=\frac{y-3}{-2}=\frac{z}{1}\cdot \)

b) Đúng.

Gọi \(M=\left( x;y;z \right)\) ta có \(\overrightarrow{AM}=\left( x-10;y-3;z \right)\), \(\left| {\vec{u}} \right|=3\).

Giả sử sau \(t\) giây kể từ lúc xuất phát \((t\ge 0),\) cabin đến vị trí điểm \(M.\)

Khi đó \(\overrightarrow{AM}=\frac{4,5t}{\left| {\vec{u}} \right|}.\vec{u}\Leftrightarrow \overrightarrow{AM}=1,5t.\vec{u}\Leftrightarrow \left\{ \begin{align}  & x-10=3t \\  & y-3=-3t \\  & z=\frac{3}{2}t \\ \end{align} \right.\)

Suy ra tọa độ của điểm \(M\) là \(\left( 3t+10;-3t+3;\frac{3t}{2} \right)\cdot \)

c) Đúng.

Cabin dừng ở điểm \(B\) có hoành độ \({{x}_{B}}=550.\)

Từ phương trình chính tắc là \(\frac{x-10}{2}=\frac{y-3}{-2}=\frac{z}{1}\) và \({{x}_{B}}=550\).

Suy ra \({{y}_{B}}=-537\) và \({{z}_{B}}=270\).

\(\begin{array}{*{35}{l}}   AB & =\sqrt{{{({{x}_{B}}-10)}^{2}}+{{\left( {{y}_{B}}-3 \right)}^{2}}+z_{B}^{2}}  \\   {} & =\sqrt{{{(540-10)}^{2}}+{{\left( -537-3 \right)}^{2}}+{{270}^{2}}}=810.  \\\end{array}\)

Quãng đường \(AB\) có độ dài bằng \(810\text{ }(\text{m)}\).

d) Sai.

Đường cáp \(AB\) có véctơ chỉ phương là \(\vec{u}=\left( 2;-2;1 \right)\).

Mặt phẳng \(\left( Oxy \right)\) có phương trình \(z=0\), có vectơ pháp tuyến \(\overrightarrow{n}=\left( 0;0;1 \right)\).

\(\sin \left( AB,O\,xy \right)=\frac{\left| \overrightarrow{u}.\overrightarrow{n} \right|}{\left| \overrightarrow{u} \right|.\left| \overrightarrow{n} \right|}=\frac{\left| 2.0-2.0+1.1 \right|}{\sqrt{5}.1}=\frac{1}{\sqrt{5}}.\)

Đường cáp \(AB\) tạo với mặt \(\left( Oxy \right)\) một góc \(27{}^\circ \) (làm tròn đến hàng đơn vị của độ).

a) Đúng.

Vì: \(x\left( 3 \right)-x\left( 0 \right)=6-3\ln 4=6-6\ln 2\approx 1,84m\). Nên quãng đường mà vật đi được trong \(3\) giây đầu tiên là \(1,84m\).

b) Đúng.

Vì: \(v\left( t \right)={x}'\left( t \right)=2-\frac{3}{t+1}\) và \(v\left( 0,5 \right)=0\) nên hạt đứng yên tại thời điểm \(t=0,5\text{s}\).

c) Đúng.

Vì: \(v\left( t \right)={x}'\left( t \right)=2-\frac{3}{t+1}\).

d) Sai.

Vì: \(v\left( 0 \right)=-1\,m/s\) nên vận tốc ban đầu của hạt là \(-1\,m/s\) (dấu âm biểu thị hạt di chuyển ngược chiều dương).

a) Sai.

Từ đồ thị hàm số\(y={f}'\left( x \right)\)ta có bảng biến thiên của hàm số \(y=f\left( x \right)\) như sau:

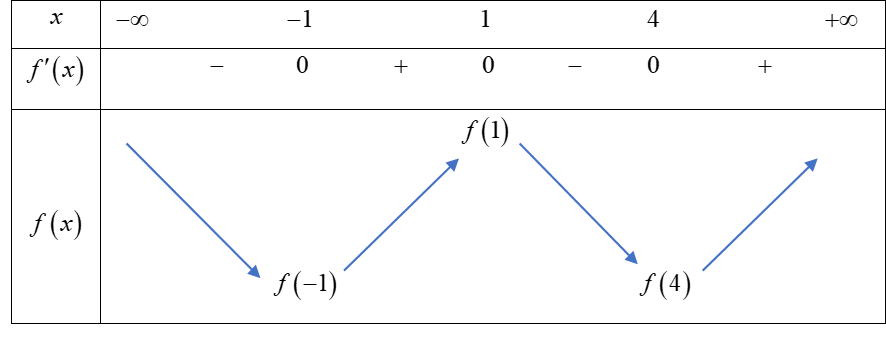
Dựa vào bảng biến thiên hàm số\(y=f\left( x \right)\) đồng biến trên các khoảng\(\left( -1;1 \right)\) và \(\left( 4;+\infty  \right)\).

b) Đúng.

Dựa vào bảng biến thiên, trên đoạn \(\left[ -1;4 \right]\) thì giá trị lớn nhất của hàm số \(y=f\left( x \right)\) là \(f\left( 1 \right)\).

c) Đúng.

Dựa vào bảng biến thiên, hàm số \(y=f\left( x \right)\) nghịch biến trên đoạn \(\left[ 1;4 \right]\), do vậy \(f\left( 1 \right)>f\left( 2 \right)>f\left( 4 \right)\).

d) Sai.

Dựa vào bảng biến thiên, hàm số \(y=f\left( x \right)\) có ba điểm cực trị.

Xét tam giác \(ABC\) có:

\(AB=BC\) (tứ giác \(ABCD\) là hình thoi).

\(\widehat{ABC}=180{}^\circ -\widehat{DAB}=180{}^\circ -120{}^\circ =60{}^\circ \).

\(\Rightarrow\) Tam giác \(ABC\) đều.

\(\Rightarrow AB=BC=AC=2024\).

Ta có: \(CO\bot BD\) (tứ giác \(ABCD\) là hình thoi).

\(CO\bot SO\) (do \(SO\bot \left( ABCD \right)\)).

\(\Rightarrow CO\bot \left( SBD \right)\).

\(\Rightarrow d\left( C,\left( SBD \right) \right)=CO=\frac{AC}{2}=\frac{2024}{2}=1012\).