Câu hỏi:

+ Gọi \(I\) là trung điểm của \(AB,AB=2\sqrt{3}\).

+ Ta có \(I(1;2;0)\), \(R=\frac{AB}{2}=\sqrt{3}\) là tâm và bán kính mặt cầu đường kính AB.

+ Mặt cầu đường kính AB có phương trình là:

\({{(x-1)}^{2}}+{{(y-2)}^{2}}+{{z}^{2}}=3\).

a) Đúng.

Ta có: 

\(\begin{array}{*{35}{l}}   {} & f(x)-g(x) & =0  \\    \Leftrightarrow  & {{x}^{2}}-2x-1-(2x-4) & =0  \\    \Leftrightarrow  & {{x}^{2}}-4x+3 & =0  \\    \Leftrightarrow  & \left[ \begin{array}{*{35}{l}}   x=1  \\    x=3  \\ \end{array} \right. & {}  \\ \end{array}\)

Vậy phương trình \(f(x)-g(x)=0\) có hai nghiệm phân biệt.

b) Sai.

Vì phương trình có 2 nghiệm \(x=1\) và \(x=3\), nên ta có trục xét dấu của \(f(x)-g(x)\) như sau:

Suy ra hiệu \(f(x)-g(x)<0\) với mọi \(x\in (1;3)\).

c) Đúng.

Để kiểm tra \(Q(x)\) có là một nguyên hàm của hàm số \(f(x)-g(x)\) hay không. Ta có thể kiểm tra bằng cách tính đạo hàm của \(Q(x)\) và so sánh xem kết quả có đúng bằng \(f(x)-g(x)\) hay không.

Ta có \(Q{{(x)}^{\prime }}={{\left( \frac{{{x}^{3}}}{3}-2{{x}^{2}}+3x \right)}^{\prime }}\) \(={{x}^{2}}-4x+3=f(x)-g(x)\).

Suy ra hàm số \(Q(x)\) là một nguyên hàm của hàm số \(f(x)-g(x)\).

d) Đúng.

+) \({{Q}_{1}}-{{Q}_{3}}=\frac{4}{3}\).

+) Hình phẳng \((H)\) được giới hạn bởi các đồ thị hàm số \(f(x)\) và \(g(x)\) và các đường \(x=1,x=3\) sẽ có diện tích là:

 Cách 1:

\(\begin{array}{*{35}{l}}   S & =\int_{1}^{3}{|}f(x)-g(x)|dx=\left| \int_{1}^{3}{\left( {{x}^{2}}-4x+3 \right)}dx \right|=\left| \left( \frac{{{x}^{3}}}{3}-2{{x}^{2}}+3x \right) \right|_{1}^{3}  \\    {} & =\left| 0-\frac{4}{3} \right|=\frac{4}{3}=Q(1)-Q(3).  \\ \end{array}\)

 Cách 2:

\(S=\int_{1}^{3}{|}f(x)-g(x)|dx\)\(=-\int_{1}^{3}{(f(}x)-g(x))dx\).

(vì \(f(x)-g(x)<0\) với mọi \(x\in (1;3)\))

\(S=-Q(x)|_{1}^{3}=-[Q(3)-Q(1)]=Q(1)-Q(3)\).

a) Đúng.

Dựa vào hình vẽ ta thấy \(H(3)=H(7)=0\).

b) Sai.

Quả bóng được thả tại thời điểm \(t=0\), nên để tìm độ cao quả bóng ta cần đi tìm \(H(0)\).

Vì hàm số liên tục tại \(t=3\) nên \(\underset{t\to 3}{\mathop{\lim }}\,H(t)=H(3)=0\) \(\Leftrightarrow -{{5.3}^{2}}+c=0\Leftrightarrow c=45\).

Vậy \(H(0)=45\). Do đó, quả bóng được thả từ độ cao \(45\text{m}\).

c) Sai.

Ta có:

\(\begin{align}  & \left\{ \begin{array}{*{35}{l}}   H(3)=0  \\    H(7)=0  \\ \end{array} \right. \\  & \Leftrightarrow \left\{ \begin{array}{*{35}{l}}   -{{5.3}^{2}}+3d+e=0  \\    -{{5.7}^{2}}+7d+e=0  \\ \end{array} \right. \\  & \Leftrightarrow \left\{ \begin{array}{*{35}{l}}   d=50  \\    e=-105  \\ \end{array} \right. \\ \end{align}\)

Vậy \(H(t)=-5{{t}^{2}}+50t-105\).

d) Đúng.

Độ cao của quả bóng sau lần nảy đầu tiên trong khoảng thời gian \(t\in [3;7]\) nên sẽ được mô tả bởi \(H(t)=-5{{t}^{2}}+50t-105\).

Khảo sát hàm số \(H(t)\) trên đoạn [3; 7].

\({{H}^{\prime }}(t)=-10t+50=0\)\(\Leftrightarrow t=5(\text{tm})\).

Ta có \(H(3)=H(7)=0\); \(H(5)=20\).

Vậy độ cao lớn nhất mà quả bóng đạt được sau lần nảy đầu tiên là \(20\text{m}\).

a) Đúng.

Ta có: \(A(0;-4;0),B(4\sqrt{3};0;0),C(0;4;0)\),

\({{A}^{\prime }}(0;-4;10),{{B}^{\prime }}(4\sqrt{3};0;9),{{C}^{\prime }}(0;4;8)\).

b) Đúng.

Ta có \(\overrightarrow{{{A}^{\prime }}{{B}^{\prime }}}=(4\sqrt{3};4;-1);\overrightarrow{{{A}^{\prime }}{{C}^{\prime }}}=(-4\sqrt{3};4;-1)\).

Vectơ pháp tuyến của mặt phẳng \(\left( {{A}^{\prime }}{{B}^{\prime }}{{C}^{\prime }} \right)\) là:

\(\vec{n}=\left[ \overrightarrow{{{A}^{\prime }}{{B}^{\prime }}},\overrightarrow{{{A}^{\prime }}{{C}^{\prime }}} \right]=(0;8\sqrt{3};32\sqrt{3})\)\(=8\sqrt{3}(0;1;4)\).

Suy ra phương trình mặt phẳng \(\left( {{A}^{\prime }}{{B}^{\prime }}{{C}^{\prime }} \right)\) là: \(y+4z-36=0\).

c) Sai.

Vectơ pháp tuyến của mặt phẳng \((ABC)\) là \(\vec{k}=(0;0;1)\).

Khi đó:

\(\cos \left( (ABC),\left( {{A}^{\prime }}{{B}^{\prime }}{{C}^{\prime }} \right) \right)=\frac{|5|}{\sqrt{{{4}^{2}}+{{1}^{2}}}}=\frac{4}{\sqrt{17}}\).

\(\to \left( (ABC),\left( {{A}^{\prime }}{{B}^{\prime }}{{C}^{\prime }} \right) \right)\approx {{14}^{{}^\circ }}\).

Vậy độ dốc của mái khoảng \({{14}^{{}^\circ }}\), mái nhà trên không ở mức tiêu chuẩn.

d) Đúng.

Gọi \(I(a;b;c)\Rightarrow \left\{ \begin{array}{*{35}{l}}   b+4c=36  \\    {{a}^{2}}+{{(b+4)}^{2}}+{{(c-10)}^{2}}={{(a-4\sqrt{3})}^{2}}+{{b}^{2}}+{{(c-9)}^{2}}  \\    {{a}^{2}}+{{(b+4)}^{2}}+{{(c-10)}^{2}}={{a}^{2}}+{{(b-4)}^{2}}+{{(c-8)}^{2}}  \\ \end{array} \right.\)

Suy ra \(I(\sqrt{5};0;9)\Rightarrow \) điểm I cách mặt sàn một khoảng là 9 mét.

a) Đúng.

Ta có \(\mathrm{P}(\mathrm{A})=0,7 ; \mathrm{P}(\mathrm{B} \mid \mathrm{A})=0,2 ; \mathrm{P}(\mathrm{B} \mid \overline{\mathrm{A}})=0,3\).

b) Sai.

Do đó \(\mathrm{P}(\overline{\mathrm{A}})=1-\mathrm{P}(\mathrm{A})=0,3\);

\(\mathrm{P}(\overline{\mathrm{B}} \mid \mathrm{A})=1-\mathrm{P}(\mathrm{B} \mid \mathrm{A})=0,8 ;\)

\(\mathrm{P}(\overline{\mathrm{B}} \mid \overline{\mathrm{A}})=1-\mathrm{P}(\mathrm{B} \mid \overline{\mathrm{A}})=0,7\).

Áp dụng công thức nhân xác suất, ta có xác suất trời nắng vào thứ Bảy và trời mưa vào Chủ nhật là:

\(\mathrm{P}(\mathrm{AB})=\mathrm{P}(\mathrm{~A}) \mathrm{P}(\mathrm{~B} \quad \mathrm{~A})=0,7 \cdot 0.2=0,14 .\)

Tương tự, ta có:

\(\begin{align}& \mathrm{P}(\mathrm{~A} \overline{\mathrm{~B}})=\mathrm{P}(\mathrm{~A}) \cdot \mathrm{P}(\overline{\mathrm{~B}} \mid \mathrm{A})=0,7 \cdot 0,8=0,56 ; \\& \mathrm{P}(\overline{\mathrm{~A}} \mathrm{~B})=\mathrm{P}(\overline{\mathrm{~A}}) \cdot \mathrm{P}(\mathrm{~B} \mid \overline{\mathrm{A}})=0,3 \cdot 0,3=0,09 ; \\& \mathrm{P}(\overline{\mathrm{~A}} \overline{\mathrm{~B}})=\mathrm{P}(\overline{\mathrm{~A}}) \cdot \mathrm{P}(\overline{\mathrm{~B}} \mid \overline{\mathrm{A}})=0,3 \cdot 0,7=0,21 .\end{align}\)

Ta có thể biểu diễn các kết quả trên theo sơ đồ cây như sau:

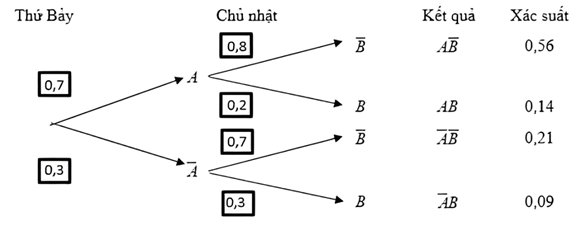c) Sai.

Xác xuất ngày chủ nhật nắng là:

\(\mathrm{P}(\overline{\mathrm{~B}})=\mathrm{P}(\mathrm{~A} \overline{\mathrm{~B}})+\mathrm{P}(\overline{\mathrm{~A}} \overline{\mathrm{~B}})=0,77=77 \% .\)

d) Sai.

Xác xuất chủ nhật trời mưa là \(P(B)=0,14+0,09=0,23\).

Ta có: \(\mathrm{P}(\mathrm{A} \mid \mathrm{B})=\frac{\mathrm{P}(\mathrm{AB})}{\mathrm{P}(\mathrm{B})}=\frac{0,14}{0,23} \approx 60,86 \%\).