Cho cấp số nhân \(\left( {{u}_{n}} \right)\) với \({{u}_{1}}=2\) và công bội \(q=3\). Giá trị của \({{u}_{2}}\) bằng:

Đáp án A đúng theo quy tắc hình hộp.

Đáp án C đúng theo quy tắc hình hộp.

Đap án D đúng theo quy tắc hình bình hành.

Đáp án B sai.

Từ bảng biến thiên, ta thấy giá trị cực tiểu của hàm số đã cho bằng -4.

Điều kiện \(x\in \left( -\infty ;-\sqrt{2} \right)\cup \left( -1;1 \right)\cup \left( \sqrt{2};+\infty  \right)\).

Vì \(\underset{x\to +\infty }{\mathop{\text{lim}}}\,y=\underset{x\to -\infty }{\mathop{\text{lim}}}\,y=\underset{x\to \pm \infty }{\mathop{\text{lim}}}\,\frac{{{x}^{2}}+3x+2}{\sqrt{{{x}^{4}}-3{{x}^{2}}+2}}=\underset{x\to \pm \infty }{\mathop{\text{lim}}}\,\frac{1+\frac{3}{x}+\frac{2}{{{x}^{2}}}}{\sqrt{1-\frac{3}{{{x}^{2}}}+\frac{2}{{{x}^{4}}}}}=1\).

nên \(y=1\) là đường tiệm cận ngang của đồ thị hàm số.

Vì \(\underset{x\to -\sqrt{2}}{\mathop{\text{lim}}}\,y=+\infty \) nên \(x=-\sqrt{2}\) là đường tiệm cận đứng của đồ thị hàm số.

Vì

\(\begin{array}{*{35}{l}}   \underset{x\to -{{1}^{+}}}{\mathop{\text{lim}}}\,y & =\underset{x\to -{{1}^{+}}}{\mathop{\text{lim}}}\,\frac{\left( x+1 \right)\left( x+2 \right)}{\sqrt{\left( x+1 \right)\left( x+\sqrt{2} \right)\left( x-1 \right)\left( x-\sqrt{2} \right)}}  \\   {} & =\underset{x\to -{{1}^{+}}}{\mathop{\text{lim}}}\,\frac{\sqrt{x+1}\left( x+2 \right)}{\sqrt{\left( x+\sqrt{2} \right)\left( x-1 \right)\left( x-\sqrt{2} \right)}}  \\   {} & =0.  \\\end{array}\)

nên \(x=-1\) không là đường tiệm cận đưng của đồ thị hàm số.

Vì \(\underset{x\to {{1}^{-}}}{\mathop{\text{lim}}}\,y=+\infty \) nên \(x=1\) là đường tiệm cận đứng của đồ thị hàm số.

Vì \(\underset{x\to {{\sqrt{2}}^{+}}}{\mathop{\text{lim}}}\,y=+\infty \) nên \(x=\sqrt{2}\) là đường tiệm cận đứng của đồ thị hàm số.

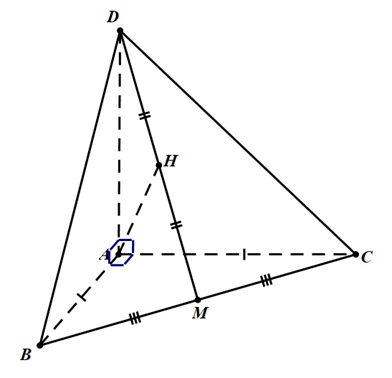
a) Đúng.

\(\overrightarrow{DM}=\frac{\overrightarrow{DB}+\overrightarrow{\text{DC}}}{2}\Rightarrow \overrightarrow{DM}=\frac{\overrightarrow{BD}+\overrightarrow{\text{CD}}}{-2}\).

b) Sai.

\(\overrightarrow{AH}=\frac{\overrightarrow{AM}+\overrightarrow{AD}}{2}\), \(\overrightarrow{AM}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}\).

\(\Rightarrow \overrightarrow{AH}=\frac{\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}+\overrightarrow{AD}}{2}\)\(\Rightarrow \overrightarrow{AH}=\frac{\overrightarrow{AD}}{2}+\frac{\overrightarrow{AB}+\overrightarrow{AC}}{4}\).

c) Đúng.

\(\begin{array}{*{35}{l}}   \overrightarrow{AB}\cdot \overrightarrow{AH} & =\overrightarrow{AB}\cdot \left( \frac{\overrightarrow{AD}}{2}+\frac{\overrightarrow{AB}+\overrightarrow{AC}}{4} \right)  \\   {} & =\frac{\overrightarrow{AB}\cdot \overrightarrow{AD}}{2}+\frac{\overrightarrow{AB}\cdot \overrightarrow{AB}+\overrightarrow{AB}\cdot \overrightarrow{AC}}{4}  \\   {} & =\frac{A{{B}^{2}}}{4}=\frac{{{a}^{2}}}{4}.  \\\end{array}\)

d) Sai.

\(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB},\overrightarrow{AH}=\frac{\overrightarrow{AD}}{2}+\frac{\overrightarrow{AB}+\overrightarrow{AC}}{4}\).

Vậy \(\overrightarrow{BC}\cdot \overrightarrow{AH}=\left( \overrightarrow{AC}-\overrightarrow{AB} \right)\cdot \left( \frac{\overrightarrow{AD}}{2}+\frac{\overrightarrow{AB}+\overrightarrow{AC}}{4} \right)\).

\(\overrightarrow{BC}\cdot \overrightarrow{AH}=\frac{\overrightarrow{AC}\cdot \overrightarrow{AD}}{2}+\frac{\overrightarrow{AC}\cdot \overrightarrow{AB}+\overrightarrow{AC}\cdot \overrightarrow{AC}}{4}-\frac{\overrightarrow{AD}\cdot \overrightarrow{AB}}{2}-\frac{\overrightarrow{AB}\cdot \overrightarrow{AB}+\overrightarrow{AB}\cdot \overrightarrow{AC}}{4}\)\(\overrightarrow{BC}\cdot \overrightarrow{AH}=\frac{\overrightarrow{AC}\cdot \overrightarrow{AC}}{4}-\frac{\overrightarrow{AB}\cdot \overrightarrow{AB}}{4}=0\).

Vậy góc giữa vectơ \(\overrightarrow{AH}\) và \(\overrightarrow{BC}\) bằng \({{90}^{\circ }}\).

Giải cách khác:

\(\left. \begin{array}{*{35}{l}}   BC\bot AM  \\   BC\bot AD  \\\end{array} \right\}\Rightarrow BC\bot \left( ACM \right)\Rightarrow BC\bot AH\Rightarrow \left( \overrightarrow{AH},\overrightarrow{BC} \right)={{90}^{\circ }}\).

Gọi \(A\) là biến cố "Học sinh được chọn là học sinh nam" thì \(\overline{A}\) là biến cố "Học sinh được chọn là học sinh nữ";

\(B\) là biến cố: "Học sinh được chọn là học sinh biết bơi" thì \(\overline{B}\) là biến cố: "Học sinh được chọn là học sinh không biết bơi".

Theo giả thiết ta có:

\(P\left( A \right)=\frac{30}{50}=\frac{3}{5}\) và \(P\left( \overline{A} \right)=\frac{50-30}{50}=\frac{2}{5}\).

\(P\left( B\mid A \right)=60\text{ }\!\!%\!\!\text{ }=\frac{3}{5}\) và \(P\left( B\mid \overline{A} \right)=50\text{ }\!\!%\!\!\text{ }=\frac{1}{2}\).

a) Xác suất học sinh được chọn là nam bằng \(P\left( A \right)=\frac{3}{5}\).

b) Xác suất học sinh được chọn là học sinh biết bơi, biết học sinh này là nam bằng \(P\left( B\mid A \right)=\frac{3}{5}\).

c) Xác suất học sinh được chọn là học sinh biết bơi là:

\(P\left( B \right)=P\left( B\mid A \right)P\left( A \right)+P\left( B\mid \overline{A} \right)P\left( \overline{A} \right)=\frac{3}{5}\cdot \frac{3}{5}+\frac{1}{2}\cdot \frac{2}{5}=\frac{14}{25}.\)

Học sinh được chọn là học sinh biết bơi thì xác suất học sinh đó là học sinh nam bằng:

\(P\left( A\mid B \right)=\frac{P\left( B\mid A \right)P\left( A \right)}{P\left( B \right)}=\frac{\frac{3}{5}\cdot \frac{3}{5}}{\frac{14}{25}}=\frac{9}{14}\).

d) Vì \(P\left( B\mid A \right)=\frac{3}{5}\) nên \(P\left( \overline{B}\mid A \right)=1-P\left( B\mid A \right)=1-\frac{3}{5}=\frac{2}{5}\).

Mặt khác, \(P\left( B \right)=\frac{14}{25}\) nên \(P\left( \overline{B} \right)=\frac{11}{25}\).

Do đó, theo công thức Bayes, xác suất để học sinh được chọn là nam khi biết học sinh đó không biết bơi là:

\(P\left( A\mid \overline{B} \right)=\frac{P\left( \overline{B}\mid A \right)P\left( A \right)}{P\left( \overline{B} \right)}=\frac{\frac{2}{5}\cdot \frac{3}{5}}{\frac{11}{25}}=\frac{6}{11}\).