Câu hỏi:
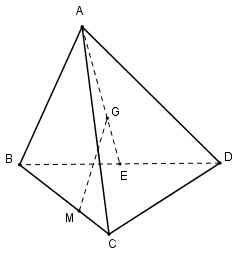
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mp(GAD) cắt tứ diện theo một thiết diện có diện tích bằng:
Đáp án đúng: a
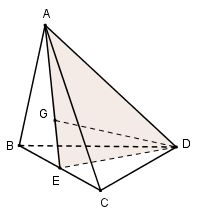
Gọi E là trung điểm của BC dễ thấy AED là thiết diện của hình chóp khi cắt bởi mp(GAD).
Ta có tam giác ABC và tam giác BCD là tam giác đều cạnh a nên \(AE=DE=\dfrac{a\sqrt{3}}{2}.\)
AD = a.
Gọi H là trung điểm của AD suy ra \(EH \bot AD\). Ta có:
\(\begin{array}{l}EH = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 2 }}{2}\\ \Rightarrow {S_{EAD}} = \frac{1}{2}EH.AD = \dfrac{1}{2}\frac{{a\sqrt 2 }}{2}.a = \dfrac{{{a^2}\sqrt 2 }}{4}\end{array}\)
Chọn A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Giữa Học Kì I - Toán 11 - Các Trường THPT Trên Toàn Quốc không chỉ giúp học sinh củng cố kiến thức đã học mà còn rèn luyện khả năng tư duy logic và giải quyết vấn đề nhanh chóng, chính xác. Đề thi bao gồm các dạng bài tập đa dạng để các em chuẩn bị tốt cho kỳ thi khác.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026