Câu hỏi:
Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm Người ta đo được khoảng cách \(AB = 40\) m, \(\widehat {CAB} = {45^ \circ },\,\widehat {CBA} = {70^ \circ }\). Tính khoảng cách A (kết quả làm tròn đến hàng phần mười của mét).
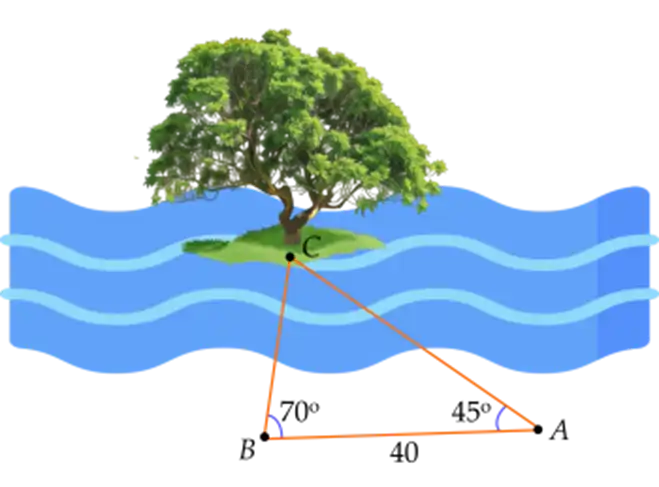
Đáp án đúng: 41,5
Ta có: \(\widehat {ACB} = {180^ \circ } - {45^ \circ } - {70^ \circ } = {65^ \circ }\)
Áp dụng hệ quả định lí sin trong tam giác ABC ta có:
\(\frac{{AC}}{{{\rm{sin}}B}} = \frac{{AB}}{{{\rm{sin}}C}}\)\( \Rightarrow \frac{{AC}}{{{\rm{sin}}{{70}^ \circ }}} = \frac{{40}}{{{\rm{sin}}{{65}^ \circ }}}\)\( \Rightarrow AC = \frac{{40}}{{{\rm{sin}}{{65}^ \circ }}}.{\rm{sin}}{70^ \circ } \approx 41,5\) (m)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Giữa Học Kì I - Toán 10 - Cánh Diều - Bộ Đề 01 là bộ test giúp học sinh hệ thống hóa và ôn luyện kiến thức trọng tâm trong chương trình Toán 10 theo bộ sách Cánh Diều, bao gồm các nội dung: Tập Hợp. Mệnh Đề, Bất Phương Trình Và Hệ Bất Phương Trình Bậc Nhất Hai Ẩn, Hệ Thức Lượng Trong Tam Giác. Định Lý Cosin. Định Lý Sin. Công Thức Tính Diện Tích Tam Giác. Giải Tam Giác, và Vectơ. Bộ đề được thiết kế với ba phần chính: Câu Trắc Nghiệm Nhiều Phương Án Lựa Chọn, Câu Trắc Nghiệm Đúng Sai, và Câu Trắc Nghiệm Trả Lời Ngắn, giúp học sinh rèn luyện khả năng tư duy, phân tích và vận dụng linh hoạt kiến thức vào bài làm. Đây là tài liệu ôn tập hiệu quả, hỗ trợ học sinh tự tin trước kỳ kiểm tra giữa học kỳ, đồng thời là nguồn tham khảo hữu ích cho giáo viên trong quá trình giảng dạy và đánh giá năng lực học sinh.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026
