Câu hỏi:
Tính giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = - x + 4y\) với (x;y) thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 1\\x \le 2\\y \ge 0\\y \le 3\end{array} \right.\).
Đáp án đúng: -2
Ta biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 1\\x \le 2\\y \ge 0\\y \le 3\end{array} \right.\) như sau:
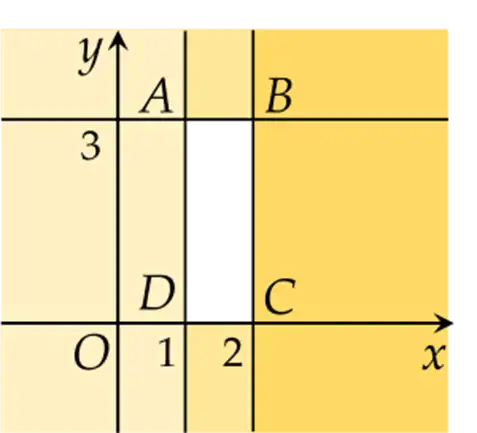
Từ hình vẽ nhận thấy miền nghiệm của hệ bất phương trình là miền tứ giác ABCD kể cả biên (phần không tô màu) với \(A\left( {1;3} \right)\); \(B\left( {2;3} \right)\); \(C\left( {2;0} \right)\); \(D\left( {1;0} \right)\).
Người ta chứng minh được: biểu thức \(F\left( {x;y} \right) = - x + 4y\) đạt giá trị nhỏ nhất tại các cặp số (x;y) là tọa độ một trong các đỉnh của tứ giác ABCD.
Tính giá trị của biểu thức \(F\left( {x;y} \right) = - x + 4y\) tại các cặp số (x;y) là tọa độ một trong các đỉnh của tứ giác ABCD rồi so sánh các giá trị đó ta được giá trị nhỏ nhất bằng \( - 2\) khi \(x = 2;\,y = 0\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Bộ Đề Kiểm Tra Giữa Học Kì I - Toán 10 - Kết Nối Tri Thức Với Cuộc Sống - Bộ Đề 01 cung cấp một bộ test ôn tập toàn diện giúp học sinh củng cố và kiểm tra kiến thức từ Tập Hợp. Mệnh Đề, Bất Phương Trình Và Hệ Bất Phương Trình Bậc Nhất Hai Ẩn, Hệ Thức Lượng Trong Tam Giác. Định Lý Cosin. Định Lý Sin. Công Thức Tính Diện Tích Tam Giác. Giải Tam Giác, và Vectơ. Đề kiểm tra được chia thành ba phần chính: Câu Trắc Nghiệm Nhiều Phương Án Lựa Chọn, Câu Trắc Nghiệm Đúng Sai, và Câu Trắc Nghiệm Trả Lời Ngắn, giúp học sinh không chỉ kiểm tra kiến thức lý thuyết mà còn phát triển kỹ năng giải toán và vẽ đồ thị một cách chính xác. Tài liệu này rất hữu ích cho việc chuẩn bị kỳ thi giữa kỳ và giúp học sinh củng cố các kỹ năng toán học cơ bản, đồng thời là công cụ hỗ trợ hiệu quả cho giáo viên trong công tác giảng dạy và kiểm tra.
Câu hỏi liên quan
Từ giả thiết, ta suy ra tam giác ABC có \(\widehat {CAB} = {60^ \circ }\); \(\widehat {ABC} = {105^ \circ }{30^{\rm{'}}}\) và \(c = 70.\)
Khi đó \(\hat A + \hat B + \hat C = {180^ \circ }\)
\( \Leftrightarrow \hat C = {180^ \circ } - \left( {\hat A + \hat B} \right)\)\( = {180^ \circ } - {165^ \circ }{30^{\rm{'}}} = {14^ \circ }{30^{\rm{'}}}.\)
Theo định lí sin, ta có
\(\frac{b}{{{\rm{sin}}B}} = \frac{c}{{{\rm{sin}}C}}\) hay \(\frac{b}{{{\rm{sin}}{{105}^ \circ }{{30}^{\rm{'}}}}} = \frac{{70}}{{{\rm{sin}}{{14}^ \circ }{{30}^{\rm{'}}}}}\).
Do đó \(AC = b = \frac{{70.{\rm{sin}}{{105}^ \circ }{{30}^{\rm{'}}}}}{{{\rm{sin}}{{14}^ \circ }{{30}^{\rm{'}}}}} \approx 269,4\) m.
Gọi CH là khoảng cách từ C đến mặt đất.
Tam giác vuông ACH có cạnh CH đối diện với góc \({30^ \circ }\) nên
\(CH = \frac{{AC}}{2} = \frac{{269,4}}{2} = 134,7\) m.
Vậy ngọn núi cao khoảng 135 m.
Phủ định của dấu \( = \) là \( \ne \).
\(x - \frac{3}{2} \ge 2\) là mệnh đề chứa biến.
Ta có \(A = \{ x \in \mathbb{R}\,{\rm{|}}\,1 \le x < 3{\rm{\} }} = \left[ {1;3} \right)\) được biểu diễn trên trục số như sau:
\(\left\{ \begin{array}{l}x \ge 1\\2x - xy \ge 0\end{array} \right.\) không là hệ bất phương trình bậc nhất hai ẩn.
Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026
Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026
