500 câu trắc nghiệm cuối HK1 Toán 8 - CTST - Đề 2
21 câu hỏi 60 phút
Kết quả của phép cộng hai đơn thức \(2 x y^2 z\) và \(-x^2 y z\) là
Một đơn thức
Một đa thức
Một số
Không xác định
Phép cộng của hai đơn thức \(2 x y^2 z\) và \(-x^2 y z\) là \(2 x y^2 z+\left(-x^2 y z\right)=2 x y^2 z-x^2 y z\).
Danh sách câu hỏi:
Phép cộng của hai đơn thức \(2 x y^2 z\) và \(-x^2 y z\) là \(2 x y^2 z+\left(-x^2 y z\right)=2 x y^2 z-x^2 y z\).
Đơn thức \(x^6\) có bậc 6; đơn thức \(y^5\) có bậc 5 ; đơn thức \(x^4 y^4\) có bậc 8; đơn thức 1 có bậc 0.
Do đó, bậc của đa thức \(A\) là 8.
Đẳng thức \((a+2)(a-2)=a^2-4\) là hằng đẳng thức.
Các đẳng thức \(4 a^2-1=3 a ; 5 a=3 a+1 ; a^2-1=2 a+1\) không là hằng đẳng thức (vì khi ta thay \(x=0\) thì hai vế của mỗi đẳng thức không bằng nhau).
Với \(B\neq0\), \(\frac{A}{B}=\frac{-A}{-B}\).
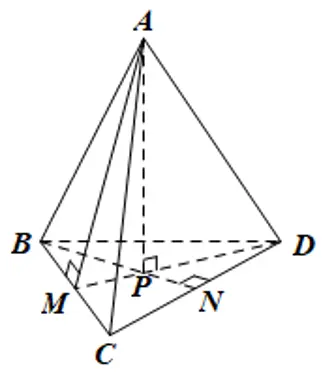
Nếu hình chóp có đáy là tam giác đều, chân đường cao trùng với trọng tâm của tam giác thì nó là hình chóp đều.
Câu 13:
Cho đa thức \(U=\left(10 x^5 y^3-25 x^3 y^2+20 x^4 y^3\right):\left(-5 x^2 y^2\right)\) và \(V=2 x^2 y(x+2)\)
Hệ số cao nhất của của đa thức \(U\) là 5
Giá trị của biểu thức \(U\) tại \(x=-1 ; y=2\) là 10
Bậc của đa thức \(V\) là 4
Tổng của hai đa thức \(U\) và \(V\) chia hết cho 5
Câu 14:
Cho tam giác \(A B C\) vuông tại \(A\). Gọi \(M\) là một điểm bất kì trên cạnh huyền \(B C\). Gọi \(D\) và \(E\) lần lượt là chân đường vuông góc kẻ từ \(M\) xuống \(A B\) và \(A C\). Lấy điểm \(I\) sao cho \(A\) là trung điểm của \(I D\); điểm \(K\) sao cho \(M\) là trung điểm của \(E K\)
\(I A=I D ; K M=K E\)
Tứ giác \(A D M E\) là hình chữ nhật
Tứ giác \(A D M C\) là hình thang cân
\(D K / / E I\)